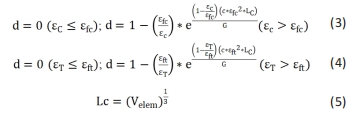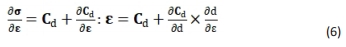不同失效模式下皮质骨结构临界能量释放率预测

doi:10.12307/2024.694

中国组织工程研究 ›› 2024, Vol. 28 ›› Issue (36): 5779-5784.doi: 10.12307/2024.694

• 数字化骨科Digital orthopedics • 上一篇下一篇

不同失效模式下皮质骨结构临界能量释放率预测

范若寻1，2，王溢童1，贾政斌3

1扬州工业职业技术学院，交通工程学院，江苏省扬州市 225000；2吉林化工学院，航空工程学院，吉林省吉林市 132022；3吉林大学，机械与航空航天工程学院，吉林省长春市 130025

收稿日期:2023-10-11 接受日期:2023-12-02 出版日期:2024-12-28 发布日期:2024-02-27
通讯作者: 范若寻，博士，副教授，扬州工业职业技术学院，交通工程学院，江苏省扬州市 225000；吉林化工学院，航空工程学院，吉林省吉林市 132022
作者简介:范若寻，男，1988年生，黑龙江省大庆市人，汉族，2016年吉林大学毕业，博士，副教授，主要从事生物固体力学研究。
基金资助:
吉林省自然科学基金(YDZJ202301ZYTS250)，项目负责人：范若寻；江苏省高等学校基础科学(自然科学)研究项目(23KJD580005)，项目负责人：范若寻

Prediction of critical energy release rate for cortical bone structure under different failure modes

Fan Ruoxun1, 2, Wang Yitong1, Jia Zhengbin3

1School of Traffic Engineering, Yangzhou Polytechnic Institute, Yangzhou 225000, Jiangsu Province, China; 2School of Aerospace Engineering, Jilin Institute of Chemical Technology, Jilin 132022, Jilin Province, China; 3School of Mechanical and Aerospace Engineering, Jilin University, Changchun 130025, Jilin Province, China

Received:2023-10-11 Accepted:2023-12-02 Online:2024-12-28 Published:2024-02-27
Contact: Fan Ruoxun, MD, Associate professor, School of Traffic Engineering, Yangzhou Polytechnic Institute, Yangzhou 225000, Jiangsu Province, China; School of Aerospace Engineering, Jilin Institute of Chemical Technology, Jilin 132022, Jilin Province, China
About author:Fan Ruoxun, MD, Associate professor, School of Traffic Engineering, Yangzhou Polytechnic Institute, Yangzhou 225000, Jiangsu Province, China; School of Aerospace Engineering, Jilin Institute of Chemical Technology, Jilin 132022, Jilin Province, China
Supported by:
Natural Science Foundation of Jilin Province, No. YDZJ202301ZYTS250 (to FRX); Basic Science (Natural Science) Research Project of Higher Education Institutions in Jiangsu Province, No. 23KJD580005 (to FRX)

摘要/Abstract

摘要：

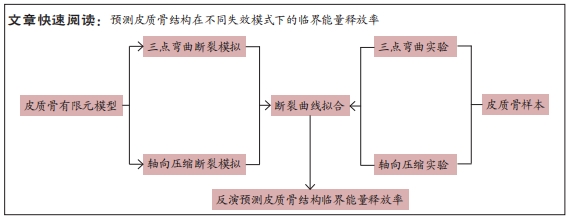
文题释义：

失效模式：具体指骨结构的断裂模式。骨结构可能会承受来自不同方向的不同类型载荷，当外界载荷超过骨结构强度极限时，骨结构将发生失效。不同类型的载荷可能会导致不同的失效模式，如弯曲失效、拉伸失效、扭转失效等，均为骨结构常见失效模式。
临界能量释放率：指结构在破坏过程中可测得的一个全局断裂力学参数，其数值是多个裂纹扩展以及塑性或脆性破坏机制共同作用的结果。当结构裂纹起始损伤中产生的能量释放率超过临界值时，裂纹继续扩展。

背景：临界能量释放率是结构在破坏过程中可测得的一个全局断裂力学参数，即使针对同一结构，在不同失效模式下其数值也可能存在差异。

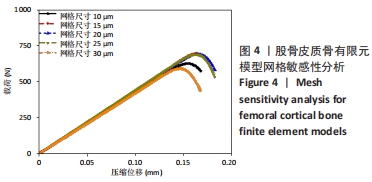
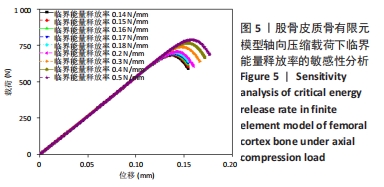
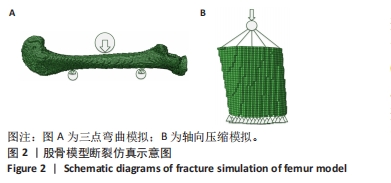
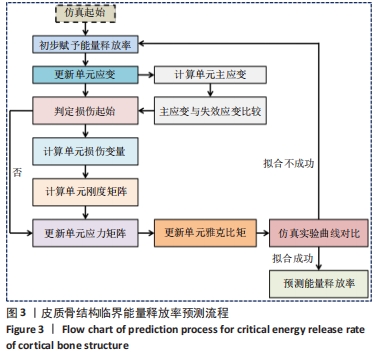
目的：提出一种方法预测皮质骨结构在不同失效模式下的临界能量释放率。
方法：针对大鼠股骨皮质骨结构进行三点弯曲与轴向压缩实验以及相应断裂仿真。通过对有限元模型赋予不同临界能量释放率进行断裂模拟，并将每次模拟所得载荷-位移曲线与实验数据进行比较，当仿真与实验所得断裂参数差异小于5%时，即代表拟合成功，以此反演预测皮质骨结构在不同失效模式下的临界能量释放率。

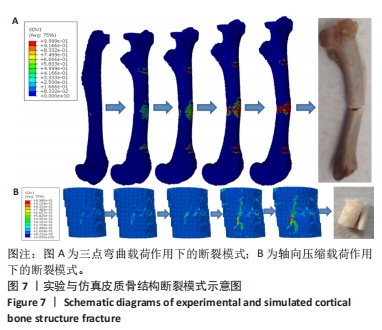
结果与结论：①结果显示大鼠股骨皮质骨结构在三点弯曲载荷下主要发生拉伸破坏，该失效模式下所预测临界能量释放率为0.16 N/mm；②在轴向压缩载荷下主要发生剪切破坏，所预测临界能量释放率为0.12 N/mm，这说明同一皮质骨结构在不同失效模式下的临界能量释放率存在差异；③此文通过对结构力学性能与损伤机制进行综合分析，揭示了不同失效模式下皮质骨结构临界能量释放率存在差异的原因，为能量释放率测量以及准确的皮质骨断裂模拟提供理论依据。

https://orcid.org/0000-0002-1604-2489 (范若寻)

中国组织工程研究杂志出版内容重点：人工关节；骨植入物；脊柱；骨折；内固定；数字化骨科；组织工程

关键词: 临界能量释放率, 皮质骨, 失效模式, 三点弯曲, 轴向压缩

Abstract: BACKGROUND: Critical energy release rate is a global fracture parameter that could be measured during the failing process, and its value may change under different failure modes even in the same structure.
OBJECTIVE: To propose an approach to predict the critical energy release rate in the femoral cortical bone structure under different failure modes.
METHODS: Three-point bending and axial compression experiments and the corresponding fracture simulations were performed on the rat femoral cortical bone structures. Different critical energy release rates were repeatedly assigned to the models to perform fracture simulation, and the predicted load-displacement curves in each simulation were compared with the experimental data to back-calculate the critical energy release rate. The successful fit was that the differences in the fracture parameters between the predicted and experimental results were less than 5%.
RESULTS AND CONCLUSION: (1) The results showed that the cortical bone structure occurred tensile open failure under three-point bending load, and the predicted critical energy release rate was 0.16 N/mm. (2) The same cortical bone structure occurred shear open failure under axial compression load, and the predicted critical energy release rate was 0.12 N/mm, which indicates that the critical energy release rate of the same cortical bone structure under different failure modes was different. (3) A comprehensive analysis from the perspectives of material mechanical properties and damage mechanism was conducted to reveal the reasons for the differences in the critical energy release rate in the cortical bone structure under different failure modes, which provided a theoretical basis for the measurement of the energy release rate and the accurate fracture simulation.

Key words: critical energy release rate, cortical bone, failure mode, three-point bending, axial compression

中图分类号:

范若寻, 王溢童, 贾政斌. 不同失效模式下皮质骨结构临界能量释放率预测[J]. 中国组织工程研究, 2024, 28(36): 5779-5784.

Fan Ruoxun, Wang Yitong, Jia Zhengbin. Prediction of critical energy release rate for cortical bone structure under different failure modes[J]. Chinese Journal of Tissue Engineering Research, 2024, 28(36): 5779-5784.

图/表（结果） 5

2.1 网格敏感性分析选取10，15，20，25，30 μm五种尺寸网格建立有限元模型，并赋予临界能量释放率0.1 N/mm进行轴向压缩模拟，以观测网格尺寸对断裂参数的影响。如图4所示，在材料输入参数相同的情况下，不同模型仿真预测所得载荷-位移曲线形状相同，但断裂参数存在差异。当网格尺寸过小或过大时，模型发生完全断裂时刻相对较早，说明网格尺寸不适合会导致结构软化率增大。当网格尺寸处于15，20，25 μm时，三者预测曲线基本重合，断裂参数也相差较小，说明这3种网格尺寸较适合建立皮质骨有限元模型进行断裂模拟。考虑到小尺寸网格相对更有利于仿真收敛，因而此文所建立有限元模型网格尺寸均选取为15 μm。

2.2 实验与仿真曲线对比分析皮质骨有限元模型的破坏过程主要由内部单元力学状态控制，而单元力学状态又与损伤变量的增速密切相关。由于在损伤变量表达式(3)或(4)中涉及到的未知材料参数只有临界能量释放率，因此其数值可通过与实验测得载荷-位移曲线进行拟合来反演预测。为保证预测精度，首先以轴向压缩断裂仿真为例，对临界能量释放率的反演预测区间进行敏感性分析。如图5所示，当临界能量释放率的反演变化间隔设置为0.01 N/mm时，不同数值下模拟得到的荷载-位移曲线几乎重合，各曲线的断裂时间差异均小于5%，由此说明反演变化间隔设置为0.01 N/mm是足够小并且合理的；同时可以看出，随着临界能量释放率从0.14 N/mm逐渐增大到0.5 N/mm，皮质骨结构发生完全断裂所需表观载荷与失效时间均有所增大；对于同一模型，在其他材料参数均相同，只有临界能量释放率不同的情况下，模型的表观弹性模量未发生变化。

图6分别展示了皮质骨结构在三点弯曲与轴向压缩载荷作用下的实验和仿真载荷-位移曲线。首先可以看出，实验样本在经历长时间的弹性阶段后，均未表现出明显的屈服阶段，而是直接从弹性阶段进入到表观断裂阶段，这说明大鼠股骨皮质骨结构在三点弯曲与轴向压缩载荷作用下均发生了准脆性断裂。然后，从不同加载模式下的实验曲线对比中可以看出，皮质骨结构在三点弯曲载荷作用下发生完全断裂时刻相对较晚，而在轴向压缩载荷作用下，皮质骨结构的表观载荷上升较快，由此可见同一皮质骨结构在不同载荷作用下的力学性能存在差异，在不同失效模式下的断裂性能也存在一定差异。最后，在断裂阶段，实验与仿真曲线无论在形状、载荷下降趋势，以及断裂时刻均较为接近，这说明在准确赋予材料参数的基础上，此文所采用的数值方法能够准确模拟皮质骨结构在三点弯曲与轴向压缩载荷下的断裂过程。

2.3 实验与仿真断裂模式对比分析图7A对比了皮质骨结构在三点弯曲载荷下的实验与仿真断裂模式，图中的“SDV1”代表单元损伤变量，可以看出二者均在股骨干中段皮质骨位置发生断裂。从仿真示意图中看出，加载初期在压头附近出现少量损伤单元，随即在支撑圆柱一侧中部出现大量损伤单元并逐渐形成主裂纹，随着弯曲程度增大，主裂纹沿横向与纵向同时扩展，逐渐扩展至压头附近，最终切断股骨中段皮质骨区域，发生拉伸失效，导致结构完全断裂。
图7B对比了皮质骨结构在轴向压缩载荷下的实验与仿真断裂模式，可以看出二者在压缩载荷下生成的主裂纹均与加载方向呈一定角度。从仿真示意图看出，压缩过程中在结构中间位置率先出现损伤单元，随着载荷增加，裂纹同时向上下扩展，并且裂纹方向逐渐与竖直方向成一定角度，直至裂纹贯穿整个结构，发生剪切失效，导致结构完全断裂。

2.4 临界能量释放率预测结果此文断裂模拟结果与有限元模型中单元损伤变量的增速密切相关。因此，能否准确拟合出实验曲线主要取决于单元损伤变量的变化趋势。损伤变量表达式(3)或(4)中除了临界能量释放率以外的其他材料输入参数均为已知值，一旦赋予在模拟过程中不会改变或可自动迭代。因此，有限元模型断裂进程仅受临界能量释放率这一个未知参数控制。通过上述反演拟合预测得到，在三点弯曲载荷失效下的皮质骨结构临界能量释放率为0.16 N/mm，在轴向压缩载荷失效下的皮质骨结构临界能量释放率为0.12 N/mm，即当分别为皮质骨结构有限元模型赋予这2个参数数值时，8个样本的仿真与实验曲线中的断裂参数差异均小于5%。

参考文献

[1] DAPAAH D, WILLETT T. A critical evaluation of cortical bone fracture toughness testing methods. J Mech Behav Biomed Mater. 2022;134:105419.
[2] 李兴国, 安兵兵, 张东升, 等. 非自相似分层次结构对骨组织断裂力学性能分析[J]. 医用生物力学,2021,36(1):30-35.
[3] NISSEN FI, ANDREASEN C, BORGEN TT, et al. Cortical bone structure of the proximal femur and incident fractures. Bone. 2022;155:116284.
[4] 杨秀芳, 孙有朝, 赵大旭, 等. 基于IMU的飞行员操纵舒适性评价研究[J]. 重庆理工大学学报,2020,34(6):111-116.
[5] WRIGHT TM, HAYES WC. Fracture mechanics parameters for compact bone-effects of density and specimen thickness. J Biomech. 1977;10:419-430.
[6] SONI A, KUMAR S, KUMAR N. Stochastic failure analysis of proximal femur using an isogeometric analysis based nonlocal gradient-enhanced damage model. Comput Meth Prog Bio. 2022;220:106820.
[7] LI S, ABDEL-WAHAB A, SILBERSCHMIDT VV. Analysis of fracture processes in cortical bone tissue. Eng Fract Mech. 2013;110:448-458.
[8] NORMAN TL, VASHISHTH D, BURR DB. Fracture toughness of human bone under tension. J Biomech. 1995;28:309-320.
[9] 安兵兵, 李凯, 张东升. 皮质骨断裂力学行为的实验研究[J]. 力学学报,2010, 42(6):1164-1171.
[10] FENG Z, RHO J, HAN S, et al. Orientation and loading condition dependence of fracture toughness in cortical bone. Mater Sci Eng C. 2000;11(1):41-46.
[11] 冯祖德. 皮质骨在拉伸型、剪切型和撕裂型加载条件下的断裂韧性──纵向断裂和横向断裂的比较[J]. 生物医学工程学杂志,1997(3):199-204.
[12] WILLETT TL, DAPAAH DY, UPPUGANTI S, et al. Bone collagen network integrity and transverse fracture toughness of human cortical bone. Bone. 2019;120:187-193.
[13] GINER E, BELDA R, ARANGO C, et al. Calculation of the critical energy release rate Gc of the cement line in cortical bone combining experimental tests and finite element models. Eng Fract Mech. 2017;184:168-182.
[14] KUMAR A, SHITOLE P, GHOSH R, et al. Experimental and numerical comparisons between finite element method, element-free Galerkin method, and extended finite element method predicted stress intensity factor and energy release rate of cortical bone considering anisotropic bone modelling. Proc Inst Mech Eng H. 2022;233(8):823-838.
[15] FAN RX, LIU J, JIA ZB. Effects of different numerical methods on the fracture prediction accuracy for cortical bone structure under bending load. Appl Sci Basel. 2023;13:3998.
[16] 范若寻. 老龄相关骨退化对骨宏微观力学性能影响的数值仿真研究[D]. 长春: 吉林大学,2016.
[17] 范若寻, 刘杰, 贾政斌. 不同数值方法模拟皮质骨结构弯曲断裂的准确性[J]. 中国组织工程研究,2024,28(12):1895-1900.
[18] FAN RX, LIU J, JIA ZB, et al. Determination of a tissue-level failure evaluation standard for rat femoral cortical bone utilizing a hybrid computational–experimental method. Proc Inst Mech Eng H. 2022;232(1):80-89.
[19] HAMBLI R. A quasi-brittle continuum damage ﬁnite element model of the human proximal femur based on element deletion. Med Biol Eng Comput. 2013;51:219-231.
[20] GAO X, CHEN MH, YANG XG, et al. Simulating damage onset and evolution in fully bio-resorbable composite under three-point bending. J Mech Behav Biomed Mater. 2018;81:72-82.
[21] GAZIANO P, FALCINELLIC, VAIRO G. A computational insight on damage-based constitutive modelling in femur mechanics. Eur J Mech A-Solid. 2022;93:104538.
[22] 张睿. 老龄骨退化及骨质疏松防治的多尺度试验与数值仿真研究[D]. 长春: 吉林大学,2014.
[23] FAN RX, GONG H, ZHANG R, et al. Quantification of age-related tissue-level failure strains of rat femoral cortical bones using an approach combining macrocompressive test and microfinite element analysis. J Biomech Eng. 2016;138: 041006.
[24] NORMAN TL, NIVARGIKAR SV, BURR DB. Resistance to crack growth in human cortical bone is greater in shear than in tension. J Biomech. 1996;29:1023-1031.
[25] KUMAR A, GHOSH R. A review on experimental and numerical investigations of cortical bone fracture. P I Mech Eng H. 2022;236(3):297-319.
[26] KHOR F, CRONIN DS, WATSON B. Importance of asymmetry and anisotropy in predicting cortical bone response and fracture using human body model femur in three-point bending and axial rotation. J Mech Behav Biomed Mater. 2018;87:213-229.
[27] FAN RX, LIU J, JIA ZB. Biomechanical evaluation of different strain judging criteria on the prediction precision of cortical bone fracture simulation under compression. Front Bioeng Biotech. 2023;11:1168783.
[28] ZIMMERMANN EA, LAUNEY ME, BARTH HD, et al. Mixed-mode fracture of human cortical bone. Biomaterials. 2009;30:5877-5884.
[29] NIE YQ, LI DX. Toughening amplification of microcracks in staggered composites. Eng Fract Mech. 2023;290:109475.
[30] DEMIRTAS A, TAYLOR EA, GLUDOVATZ B, et al. An integrated experimental-computational framework to assess the influence of microstructure and material properties on fracture toughness in clinical specimens of human femoral cortical bone. J Mech Behav Biomed Mater. 2023;145:106034.
[31] 许灿, 李明清, 王成功, 等. 皮质骨的多级结构与韧化机制研究进展[J]. 医用生物力学,2018,33(3):273-279.
[32] 王伟军, 刘杰, 刘军, 等. 基于不同应变判定准则模拟皮质骨断裂的准确性[J]. 中国组织工程研究,2020,24(24):3828-3833.

引言

临界能量释放率是结构在破坏过程中可测得的一个全局断裂力学参数，其数值是多个裂纹扩展以及破坏机制共同作用的结果[1]。皮质骨在自然状态下往往承受多轴载荷，其临界能量释放率可能受到结构位置与加载条件等多种因素影响，因此即使针对相同结构，在不同失效模式下测得的皮质骨临界能量释放率也可能存在差异[2-4]。WRIGHT等[5]和SONI等[6]曾测得牛股骨皮质骨的临界能量释放率分别处于0.62-1.29 N/mm和0.96-1.39 N/mm，而LI等[7]则在相同位置牛皮质骨结构测得临界能量释放率处于4.0-5.0 N/mm之间。
皮质骨结构的临界能量释放率可通过实验测量。
NORMAN等[8-10]在早期研究了皮质骨的断裂性能并计算其临界能量释放率，随后研究人员先后在不同失效模式下的断裂实验中测量了皮质骨结构的临界能量释放率。不同形状的皮质骨样本，如双悬臂梁、压缩拉伸试样等也被用来测量临界能量释放率[11-12]。上述实验结果显示，即使针对同一部位的皮质骨进行实验，测试结果往往也存在一定差异，这说明临界能量释放率对于测试方法与失效模式较为敏感。为观察样本断裂前后内部力学状态，研究人员开始采用有限元方法模拟皮质骨结构在不同载荷下的断裂过程，并预测临界能量释放率。GINER等[13-14]分别模拟了牛胫骨皮质骨结构的断裂过程并预测其临界能量释放率。仿真研究虽能够准确模拟皮质骨结构的断裂过程，但却需提前设定结构断裂路径或者存在计算代价过高而不适合三维骨结构断裂模拟的问题，这对于预测皮质骨结构的临界能量释放率造成一定阻碍。
基于此，此文拟结合实验测试与有限元分析，提出一种预测皮质骨结构临界能量释放率的方法。首先针对大鼠股骨皮质骨结构进行三点弯曲与轴向压缩实验，并进行相应的断裂仿真分析；在模拟过程中，通过为有限元模型赋予不同的临界能量释放率进行断裂模拟，而后将每次预测所得载荷-位移曲线与实验数据进行对比，以此反演临界能量释放率数值，同时观察不同失效模式下结构临界能量释放率的变化；最后，通过对结构力学性能与损伤断裂机制进行综合分析，揭示不同失效模式下临界能量释放率存在差异的原因，以此为皮质骨结构能量释放率的获取及准确模拟提供理论依据。中国组织工程研究杂志出版内容重点：人工关节；骨植入物；脊柱；骨折；内固定；数字化骨科；组织工程

材料方法

1.1 设计大鼠股骨皮质骨结构三点弯曲与轴向压缩实验，针对相应皮质骨结构有限元模型进行三点弯曲与轴向压缩断裂仿真模拟。
1.2 时间及地点三点弯曲实验于2020年10月在生物力学实验室完成，轴向压缩实验于2021年6月在生物力学实验室完成，断裂仿真模拟于2022年6月在仿真实验室完成。
1.3 材料实验对象为8根大鼠股骨，其中4根用于三点弯曲实验，4根用于轴向压缩实验。股骨实验素材来源于健康雄性3月龄Wistar大鼠，由吉林大学实验动物中心提供，许可证号：SYXK(吉)2021-0006。大鼠首先通过吸入异氟烷(浓度5%)进行全身麻醉，然后在腹腔主动脉放血处死，而后取其左侧股骨，剔除与股骨相连的肌肉和软组织。仿真对象为与实验相对应的股骨皮质骨结构有限元模型。实验方案经吉林大学第一医院动物实验伦理委员会批准，批准号为2013-135。实验过程遵循了国际兽医学编辑协会《关于动物伦理与福利的作者指南共识》和本地及国家法规。
1.4 方法
1.4.1 轴向压缩与三点弯曲实验描述选取4根完整股骨样本置于万能试验机(AG-X plus，Shimadzu，Kyoto，Japan)进行三点弯曲实验测试，试验机压头加载位置为股骨干中段皮质骨区域，实验跨距设置为20 mm，压头以0.5 mm/min的速度匀速向下，至样本完全断裂后停止。为防止弯曲过程中股骨样本发生转动或横向滑移，特选取表面粗糙度较高的2根特制圆柱支撑结构以增大横向摩擦力，具体如图1A所
示[15]。三点弯曲实验过程中保证了4个样本在试验机压头加载位置的壁厚相近。经测量，4个样本在压头加载位置的皮质骨壁厚分别为0.94，0.91，0.92，0.91 mm。

选取另外4根股骨样本，从股骨干中间位置为起始，分别向股骨近端与远端共截取5 mm长的皮质骨结构进行轴向压缩实验，压缩速度设置为0.5 mm/min，直至样本完全断裂后停止，具体如图1B所示[16]。轴向压缩实验过程中保证4个样本在压缩处的表面积相近。根据文献[16]中的表面积公式计算，4个样本压缩处的表面积分别为20.86，21.38，20.66，20.94 mm2。

1.4.2 股骨皮质骨结构有限元模型建立针对大鼠股骨样本进行Micro-CT扫描，空间分辨率设置为18 μm。通过SKYSCAN软件获得二维连续影像，而后将其导入至MIMICS软件重构股骨几何模型，并通过ABAQUS软件应用C3D8单元建立三维股骨皮质骨有限元模型。由于此文仿真对象为股骨干中段皮质骨结构，所以大鼠股骨有限元模型仅包含外部皮质骨。在MIMICS软件中将股骨影像阈值设置为800-
2 000 HU，由此可避免选择松质骨区域图像，如此所建立股骨有限元模型不包含内部松质骨结构。

三点弯曲仿真中，为模拟实验边界条件，分别在股骨模型上、下方建立刚性圆柱，其中上方为刚性压头，下方为刚性支撑圆柱。为模拟法向载荷从压头传递至股骨，设置压头与股骨模型为无摩擦接触关系[17]。由于下方支撑刚性圆柱表面粗糙度较高，与股骨模型之间摩擦力较大，二者未发生相对位移，因此设置股骨模型与下方刚性圆柱为绑定连接。同时在上方压头施加轴向位移，并完全约束下方刚性圆柱，完成三点弯曲加载，如图2A所示。轴向压缩仿真中，在皮质骨上方建立参考点，将其与模型上表面耦合，并在参考点上施加位移载荷，约束参考点上除加载方向的其他自由度，并完全约束模型下表面自由度，完成轴向压缩加载[18]。有限元模型如图2B所示。

1.4.3 结构断裂模拟与临界能量释放率预测依据连续损伤力学理论可知，结构在准静态载荷作用下，基于损伤变量的应力-应变关系式如下[19]：
σ=Cd ε (1)
Cd=(1-d) C (2)
式中σ为应力张量，Cd为损伤弹性矩阵张量，ε为应变张量，d为损伤变量，C为弹性矩阵张量。
依据文献，并结合此文三点弯曲与轴向压缩实验实际情况，分别设置有限元模型单元在压缩与拉伸方向的损伤变表达式如下[19-21]：

式中εc与εT为单元最小与最大主应变，εfc与εft为皮质骨材料临界压缩与拉伸失效应变，c为单元加载方向刚度值，Lc为单元特征长度，G为临界能量释放率，Velem为单元体积。
加载初期，当单元受力所产生主应变小于皮质骨材料临界失效应变时，结构尚处于弹性阶段，单元刚度矩阵不变。随着弯曲载荷增大，当单元主应变超过临界失效应变时，该单元发生损伤，单元损伤变量开始随主应变上升而增大，致使单元刚度逐渐降低，同时在迭代过程中，单元雅克比矩阵也逐渐发生退化，雅克比矩阵损伤演化表达式如式(6)所示[20]。当单元损伤变量趋近于1时，单元发生失效失去承载能力。随着弯曲程度进一步加大，失效单元逐渐增多，当失效单元积累到一定数量时，皮质骨结构无法有效承载，随即发生表观断裂。

此文所模拟断裂过程主要通过编制UMAT子程序实现有限元模型中单元的损伤与失效累计。该程序可自动判定单元发生压缩或拉伸失效。在损伤变量表达式(3)或(4)中涉及到的材料参数有：单元最大与最小主应变，可在迭代过程中求出；皮质骨组织弹性模量，其值已由课题组前期针对相同样本的纳米压痕实验测得，其中3月龄大鼠股骨皮质骨材料的横向弹性模量平均值为8 769 MPa，纵向弹性模量平均值为10 383 MPa[22]；3月龄大鼠股骨皮质骨材料的临界失效应变也已由课题组前期研究得到，其中皮质骨材料临界压缩失效应变为4.35%，临界拉伸失效应变为2.61%[23]；泊松比依据文献设定为0.3[16-17]；单元特征长度可在每次迭代过程中通过公式(5)由单元体积求出[19]。加载过程中，由于单元应变不断变化，所以单元体积与单元特征长度在每次迭代过程中也不断发生变化。由此可知，在损伤变量表达式(3)或(4)中，只有临界能量释放率这一个材料参数未知，即此文反演拟合所求参数。

基于此，此文预测思路为首先选取结构临界能量释放率的大致范围，依据文献可知在不同实验方法与加载模式下所测数值范围主要处于0.1-0.5 N/mm之间[24-25]。由此，仿真过程以0.1 N/mm为起始，为有限元模型赋予临界能量释放率，并以0.01的间隔逐渐递增。将应用每个能量释放率数值进行仿真所得载荷-位移曲线与实验结果对比，直至找到与实验最为接近的仿真曲线，即当仿真与实验所得断裂参数，包括强度极限与失效位移差异均小于5%时定义为拟合成功，此时所赋数值可以认为是皮质骨结构的临界能量释放率，以此反演预测得到皮质骨结构的临界能量释放率[19]。反演拟合预测流程具体如图3所示。

1.5 主要观察指标针对大鼠股骨皮质骨有限元模型进行三点弯曲与轴向压缩断裂模拟，主要观测仿真所得载荷-位移曲线以及模型断裂模式，通过将预测载荷-位移曲线与实验结果进行对比拟合，反演预测皮质骨结构临界能量释放率数值。

讨论

此次研究重点为确保有限元仿真结果的可靠性，从而保证反演预测临界能量释放率的准确。基于此，此文主要从两方面保证预测结果准确性。第一，预测结果主要受单元的损伤变量影响，因此所采用损伤变量表达式在参考文献基础上又进行了更新，涉及更多材料参数。其中，公式内的单元在加载方向刚度值，主要为了体现单元弹性模量对结构力学性能的影响，单元在加载方向的刚度值越大，损伤变量越小，结构所需断裂载荷越大；单元特征长度主要反映单元失效特性，其值越大，单元发生失效的难度相对越大，从而结构所需断裂载荷越大。第二，此文为有限元模型赋予的材料参数，多数为实验测得，其中皮质骨组织弹性模量和临界失效应变均为前期实验测得，单元特征长度与单元体积相关，通过每次迭代自动求出。因此，通过两方面保障了此文仿真预测的准确性。通过实验与仿真的断裂模式对比也可以看出，无论是三点弯曲模拟还是轴向压缩断裂模拟均与实验结果较为吻合，而且两种模拟断裂进程也均与文献描述相符[26-27]。同时依据文献所述，剪切滑移型失效模式的能量释放率相比张开型失效模式的能量释放率要低25%左右，该趋势也与此文预测结果一致[28]。
此文所预测皮质骨结构在不同失效模式下的临界能量释放率存在差异可能与微观裂纹驱动力前进方向不同有关[29]。能量释放率决定了裂纹扩展所需最低能量，因此裂纹驱动力应沿着皮质骨微观结构相对脆弱方向扩展[30]。此文皮质骨结构在两种载荷作用下所发生的断裂均属于复合型断裂，但在三点弯曲载荷下以拉伸张开型失效为主，即主要在拉应力作用下产生裂纹，且裂纹沿垂直于骨单位方向扩展，直至贯通上下表面，发生完全断裂失效；而在轴向压缩载荷下则以剪切滑移型失效为主，即在压缩应力与切应力联合作用下产生裂纹，且裂纹沿着与骨单位成一定角度的方向扩展。
在微观层面，裂纹驱动力沿骨单位方向扩展所受阻力最小，这是因为扩展时裂纹驱动力仅需破坏一根或数根骨单位即可持续扩展，整个破坏过程类似于“撕纸效应”，只要突破了骨单位最上方的阻力，裂纹即可扩展。随着裂纹扩展方向与骨单位方向夹角增大，裂纹扩展难度逐渐增大，所需裂纹驱动力也逐渐增大，这是因为裂纹扩展需突破相对多的骨单位，并可能导致裂纹在扩展路径中出现偏转和扭曲，即本来在沿夹角方向扩展过程中又改为沿骨单位方向扩展[31]。当裂纹扩展方向与骨单位方向夹角增大至90°时，即裂纹沿垂直于骨单位方向扩展，所遇阻力最大，这是由于裂纹每次扩展均需突破大量骨单位，相当于裂纹驱动力总是沿着皮质骨微观结构最强壮的位置扩展，这需要较高的裂纹驱动力才可实现[32]。因此，三点弯曲载荷作用下出现的横向裂纹扩展所需能量高于压缩载荷作用下。由于裂纹沿横向扩展时阻碍较大，裂纹驱动力可能会重新选择扩展路径，即又沿微观结构较脆弱的方向扩展，因此从图7A中可以看出在股骨中段皮质骨结构两侧也出现一定的损伤单元，但由于压头弯曲载荷加载方向的限制，每次加载新产生的裂纹驱动力又继续沿着横向前进，直至能量积攒足够，裂纹从下方贯穿上方，发生完全断裂。
此文在预测临界能量释放率的同时也存在一些不足：首先所选取样本数量不充分，无法统计得出此批次样本中大鼠股骨皮质骨结构在不同失效模式下的临界能量释放率平均值；其次，此文所选取皮质骨样本虽来自于同一批次，但各样本微观结构以及弹性模量可能仍存在一定差异，因此即使针对同一批次的样本，可能预测力学性能也会不同。虽然存在上述局限，但此文主要目的为提出一种能够准确预测皮质骨结构临界能量释放率的方法，仿真过程中所赋予皮质骨材料参数均源于实验测得，当所编制断裂模拟程序正确时，可以看出仿真结果与实验结果高度吻合，能够验证所采用模拟方法的准确性，以此达到预测结构临界能量释放率的目的。
结论：此文结果显示大鼠股骨皮质骨结构在三点弯曲载荷作用下主要发生拉伸破坏，该失效模式下所预测临界能量释放率为0.16 N/mm；在轴向压缩载荷作用下主要发生剪切破坏，该失效模式下所预测临界能量释放率为0.12 N/mm。通过对皮质骨结构力学性能与损伤机制进行分析，初步揭示其在不同失效模式下的临界能量释放率存在差异可能与断裂过程中微观裂纹驱动力前进方向不同有关。临界能量释放率是骨结构的一种整体断裂参数，对于骨折发生有决定性影响，同时针对不同载荷作用下皮质骨结构裂纹扩展模式的研究对于骨折的形成与预防也具有一定指导意义，因而此次研究结果对于骨折在临床的治疗与预防均具备参考意义。中国组织工程研究杂志出版内容重点：人工关节；骨植入物；脊柱；骨折；内固定；数字化骨科；组织工程

不同失效模式下皮质骨结构临界能量释放率预测

Prediction of critical energy release rate for cortical bone structure under different failure modes

PDF

可视化

摘要/Abstract

引用本文

使用本文

图/表（结果） 5

参考文献

相关文章 15

引言

材料方法

讨论

文章快阅

延伸阅读

编辑推荐

Metrics

本文评价

[1]	霞黑达·依拉尔江, 尼加提·吐尔逊, 热依拉·库尔班, 白布加甫·叶力思, 陈欣. 三维有限元分析不同特征骨组织中应力的分布规律[J]. 中国组织工程研究, 2024, 28(8): 1277-1282.
[2]	张连鹏, 居来提·买提肉孜, 张治豪, 张瑞, 阿卜力克木·买买提, 帕尔哈提·热西提. 皮质骨轨迹置钉在腰椎翻修中的力学分析[J]. 中国组织工程研究, 2024, 28(24): 3783-3788.
[3]	范若寻, 刘杰, 贾政斌. 不同数值方法模拟皮质骨结构弯曲断裂的准确性[J]. 中国组织工程研究, 2024, 28(12): 1895-1900.
[4]	程云忠, 刘玉增, 海涌, 关立, 潘爱星, 张希诺, 陶鲁铭, 李越. 皮质骨轨迹螺钉研究现状与发展趋势的文献计量及可视化分析[J]. 中国组织工程研究, 2023, 27(4): 513-519.
[5]	马赛, 刘波, 李楠, 何达. 机器人辅助与传统徒手置入皮质骨轨迹螺钉在老年骨质疏松性腰椎手术应用中的比较[J]. 中国组织工程研究, 2023, 27(27): 4332-4336.
[6]	陈鉴权, 陈茂水, 吕洲明, 陈荣彬, 余照宇, 刘万鹏, 林新源, 林定坤. 有限元分析皮质骨轨迹螺钉联合椎弓根螺钉固定椎体运动单元的生物力学性能[J]. 中国组织工程研究, 2023, 27(22): 3457-3462.
[7]	鄢来军, 葛海雅, 周斌, 糜大国, 王鹏翔, 李楠. 斜外侧腰椎椎间融合与双侧皮质骨轨迹螺钉置入后腰椎生物力学的有限元分析[J]. 中国组织工程研究, 2023, 27(13): 1969-1974.
[8]	蔡风, 余波, 曾铎, 陈钦灿, 廖琦. 皮质骨轨迹螺钉内固定治疗老年骨质疏松性腰椎疾病[J]. 中国组织工程研究, 2022, 26(3): 403-407.
[9]	周志豪, 阿拉法特·卡哈尔, 王轶希, 刘东山, 希尔艾力·麦麦提, 石文杰, 帕尔哈提·热西提. 传统椎弓根螺钉与改良皮质骨轨迹置钉技术的生物力学性能有限元分析[J]. 中国组织工程研究, 2022, 26(18): 2789-2794.
[10]	渠艳, 李洁银, 庄秀妹, 叶剑涛, 叶秀华. 不同气压热处理钯银合金与瓷结合的强度[J]. 中国组织工程研究, 2022, 26(16): 2526-2531.
[11]	林书, 胡豇, 万仑, 唐六一, 王跃, 俞阳. 骨科机器人辅助皮质骨轨迹螺钉内固定治疗腰椎退行性疾病[J]. 中国组织工程研究, 2022, 26(15): 2356-2360.
[12]	任航宁, 居来提·买提肉孜, 帕尔哈提·热西提, 罗辉卿. 皮质骨轨迹椎弓根系统拔出力下腰椎的有限元分析[J]. 中国组织工程研究, 2021, 25(36): 5771-5776.
[13]	魏源标, 郭惠智, 张顺聪. 皮质骨轨迹螺钉固定对相邻节段影响的有限元分析[J]. 中国组织工程研究, 2021, 25(18): 2799-2804.
[14]	汪亮, 黄朝朝, 于娇娜, 顾卫东, 王忍, 钱志艺. 桥接系统混棒与双棒结构治疗股骨及胫骨骨折的生物力学特点[J]. 中国组织工程研究, 2020, 24(6): 888-892.
[15]	王伟军, 刘杰, 刘军, 贾正斌, 范若寻. 基于不同应变判定准则模拟皮质骨断裂的准确性[J]. 中国组织工程研究, 2020, 24(24): 3828-3833.