Chinese Journal of Tissue Engineering Research ›› 2026, Vol. 30 ›› Issue (9): 2343-2349.doi: 10.12307/2025.191
Previous Articles Next Articles
Characteristics and clinical application of ankle joint finite element models
Zhang Nan, Meng Qinghua, Bao Chunyu
- New Campus of Tianjin University of Sport, Tianjin 301617, China
-
Received:2024-04-08Accepted:2024-06-11Online:2026-03-28Published:2025-09-29 -
Contact:Meng Qinghua, MD, Professor, New Campus of Tianjin University of Sport, Tianjin 301617, China -
About author:Zhang Nan, Master candidate, New Campus of Tianjin University of Sport, Tianjin 301617, China
CLC Number:
Cite this article
Zhang Nan, Meng Qinghua, Bao Chunyu. Characteristics and clinical application of ankle joint finite element models[J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2343-2349.
share this article
Add to citation manager EndNote|Reference Manager|ProCite|BibTeX|RefWorks
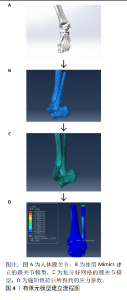
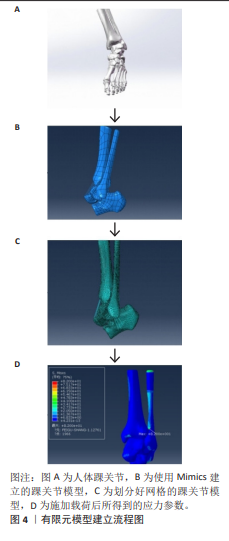
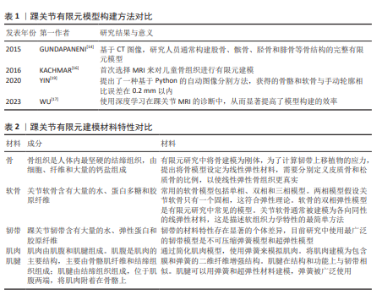
2.1 模型构建 有限元模型建立工作流程如图4所示。有限元建模的第一步是获取高质量的医学图像数据。X射线片、超声波、CT和MRI被广泛用于检测骨、关节和软组织。由于有限元模型的建立涉及到组织的三维重建,因此CT和MRI是有限元建模的主要图像数据来源。CT和MRI扫描参数与有限元的精细程度密切相关。CT和MRI的层厚通常为1 mm,最薄的CT层厚为0.5 mm。 CT图像能清晰显示骨组织的形态和病变,但软组织显示不佳。基于CT图像,研究人员通常构建股骨、髌骨、胫骨和腓骨等骨结构的有限元模型[14]。MRI图像可以清晰地显示软骨和软组织形态,用于构建软骨、韧带和肌腱的有限元模型[15],但通过MRI获得的骨组织模型不如通过CT扫描获得的模型精细。考虑到CT的辐射,一些研究者在对儿童骨组织进行有限元建模时,选择MRI来勾勒骨骼的形态[16]。CT和MRI机器的参数设置不同,如果将提取的3D结构直接连接在一起,会影响模型的准确性。一些研究人员在志愿者的踝关节上放置外部参考点,以匹配CT和MRI图像,然后通过解剖学结合踝关节的不同结构。大多数组织模型需要由专业人员使用Mimics等图像处理软件在图像上手动勾勒出轮廓,然后导入到ABAQUS、ANSYS等有限元分析软件中进行计算[17],在这个分析计算过程中,可以得到应力等参数。研究人员通过使用深度学习在踝关节MRI的诊断中,从而显著提高了模型构建的效率[18]。同样,YIN等[19]提出了一种基于Python的自动图像分割方法,获得的骨骼和软骨与手动轮廓相比误差在0.2 mm以内。一般来说,有限元轮廓需要基于高质量的图像,依赖于高性能的计算机和相关软件进行图像处理和有限元分析,半自动或全自动的有限元分割可能是一个潜在的发展方向。踝关节有限元模型构建方法对比见表1。"
2.2 材料特性 在踝关节的肌肉骨骼系统中,骨、软骨和软组织如韧带主要负责支撑身体负荷、限制关节运动和保护关节。人体远比精密的机器复杂,软组织的机械性能比大多数工程材料更先进。肌肉骨骼系统的组织由纤维、蛋白质、水和电解质组成,它们巧妙地结合在一起,给予每个组织特定的机械功能[20-21]。与渗透作用相关的蛋白聚糖,在与水结合后会影响组织的黏滞性和其他特性[22],同时胶原纤维使得其具有一定的拉伸强度。 为获得有限元模型的机械参数,需要进行生物力学实验,而温度变化会严重影响组织结构和机械性能。研究结果表明,在20 ℃时,韧带和肌腱的结构和机械性能保持不变,可以为后续的生物力学实验提供参考[23]。此外,关节的运动状态也会影响材料属性的选择,生物力学实验的静态分析适用于瞬态变化或平衡状态,可用于研究软组织在某一时刻的特征变化。 总之,在有限元建模过程中,选择合适的材料特性和材料参数可以更好地描述软组织的力学特性,这对提高有限元的精度至关重要。目前有限元研究中的材料特性主要来源于其他研究和材料试验。下面将分别描述踝关节各结构的模型材料,见表2。 2.2.1 骨 建立一个准确完整的踝关节数值模型需要结合生理载荷条件来定量确定等效应力和应变[22-32]。然而,一些早期的踝关节有限元模型被简化为仅包含骨和韧带的材料属性[23-28]。皮质骨和松质骨的材料属性被认为是一致的[23-24,26,28]。 松质骨和韧带材料属性单一的值不能准确地复制生理条件[32],在一些早期的研究中,使用更大的单元尺寸来表示脚踝足部复合体,这不足以表示踝关节的复杂几何形状 [22,27-28]。OZEN等[23]研究了整个踝关节的应力分布,结果表明,肌力对踝关节的应力分布没有显著影响;但是在他们的模型中,材料属性的单一值同时代表皮质骨和松质骨,这不能准确代表生理状况。因此,从早期研究来看,现有的模型要么缺乏适当的骨骼和韧带的材料分布,要么未准确表示骨骼的几何形状,要么没有考虑肌力。预计肌力、韧带和骨材料对构成踝关节不同骨骼的载荷传递和应力分布有影响。对材料弹性模型的选择是关键的,由于缺乏机械性能的原始数据,弹性模型往往被简化。骨通常简化为线性弹性模型,而超弹性模型通常用于软组织。当简化为均质各向同性材料时,骨的特性通常假定弹性模量为7 300 MPa, 该值来源于健康踝关节的皮质和小梁弹性模量的加权平均值[33]。一些研究已经考虑将所有骨作为皮质骨处理[34-35],而其他人使用了显著更高的未参考值[36]。一项研究比较了4种不同弹性模量(7 300,14 600,21 900,29 200 MPa)对脚和踝关节模型的影响,结果发现,弹性模量增加导致骨应力和应变降低[37]。 2.2.2 软骨 关节软骨含有大量的水、蛋白多糖和胶原纤维。关节表面的软骨厚度是可变的,将软骨简化为具有相同厚度的模型将导致软骨接触应力显著增加[38]。关节软骨是各向异性的双相材料[39],先前已经研究了软骨的双相性质[40-41]。当软骨被建模为线性弹性材料时,弹性模量和泊松比都发生了变化。弹性模量表示材料施加特定载荷所产生变形程度的大小,泊松比表示材料体积响应于载荷而压缩的程度,其中泊松比为0.5的材料是完全不可压缩的,这些值影响软骨的机械行为,进而影响模型结果。软骨已经被建模为具有比骨更低的弹性模量[42],所使用的泊松比倾向于落在0.4-0.49的范围内,这表明软骨在载荷下不会产生太大的体积变化,但它可以容易地改变形状,使其能够符合关节表面,同时提供抗冲击性。这在很大程度上被认为适合于对足部和踝部软骨进行建模;然而,当考虑软骨接触压力时,超弹性材料模型将更合适,因为它可以复制组织在负载下变形的时间依赖性。关于哪种模型最适合于踝关节有限元模型的应用,文献中没有达成一致意见,Yeoh、Neo-Hookean、Mooney-Rivlin和Ogden都使用了超弹性材料模型模型。在对模型进行的模拟中对线性弹性材料和超弹性材料模型进行了比较,通过与数学模型的验证,发现超弹性材料模型是最适合描述软骨行为的模型[43]。 2.2.3 韧带 踝关节韧带含有大量的水、弹性蛋白和胶原纤维。基质中的蛋白多糖和透明质酸可以从周围区域吸收水分以提供特定的支撑,在建模时需要考虑韧带不可压缩。由于个体差异,踝关节韧带的材料特性和生物力学响应存在群体差异。韧带通常均以相同的弹性模量模拟;最常用的是260 MPa[44];然而20 MPa和350 MPa也已在文献中报道[45-46]。为了增加复杂性,一些研究为每个韧带赋予了其自身的弹性模量,这些研究使用范围包括7.00-18.44 MPa[47],100-320 MPa和99.5-512.0 MPa[48-49]。韧带建模的另一种方法是使用线性弹簧元件,这些元件由刚度值定义;一些刚度值来自力学测试数据,但对于没有相关力学测试数据的韧带,假设刚度为70 N/mm[50]。有报道将软组织特性简化为同质各向同性线性弹性材料,然而如果将此作为研究重点,这种简化可能会影响任何足底接触压力输出[51]。 2.2.4 肌肉和肌腱 肌肉由肌腹和肌腱组成。肌腹是肌肉的主要结构,主要由骨骼肌纤维和结缔组织组成;肌腱由结缔组织组成,位于肌腹两端,将肌肉附着在骨骼上。MRI图像可以得到准确的肌肉形态。 ESRAFILIAN等 [52]简化了肌肉模型,并使用弹簧来模拟肌肉。一些学者还将肌肉建模为包含膜和弹簧的二维纤维增强结构[53]。肌腱在结构和功能上与韧带相似,可以用弹簧和超弹性材料建模,而弹簧被广泛使用[47]。WANG 等 [54] 比较了3种肌腱模型:Marlow、Neo-Hookean 和线性弹性模型,他们发现,Marlow 模型与实验力学数据更加一致。 OpenSim 软件可以建立肌肉骨骼模型。OpenSim 构建的肌肉骨骼模型可以模拟肌肉骨骼动力学和神经肌肉控制来研究关节活动,计算肌肉力量,并预测关节运动,而无需生物力学实验,但是其不能计算关节接触力学 [55]。有限元模型是肌肉骨骼模型一个很好的补充,两种模型的结合可用于分析踝关节的动态生物力学 [54]。OpenSim 的优化工具箱可用于评估肌肉力量,以生成特定的 FRPE 模型 [56]。肌电图可用于建立肌肉骨骼模型。研究人员比较了不同肌肉骨骼模型预测关节运动的可靠性,肌电图辅 助的肌肉骨骼模型能够更好地评估踝关节的运动学和应力载荷分布 [57]。肌电信号的肌肉骨骼模型能够实现更准确的预测,并可应用于踝关节动力学研究 [58-59]。 肌肉骨骼模型提供了肌肉力和踝关节运动学之间相 互作用的非侵入性数据,而这在实验室中是无法测量的。肌肉骨骼模型与有限元法的结合为解决复杂的生物力学问题提供了途径,将踝关节的有限元研究提升到一个新 的水平。 2.2.5 接触条件 有限元法涉及多个结构之间的接触。根据解剖关系组合相应的结构,可使模型分析结果更可靠。接触摩擦是踝关节有限元研究中的一个挑战性问题。关节内的摩擦系数很低,大多数踝关节有限元模型都假设关节内没有摩擦。有人认为,踝关节在关节液润滑和软骨水的作用下摩擦系数约为0.01[60],一些研究认为摩擦系数为0.02[61]。有限元软件提供了各种模拟无摩擦和摩擦接触的算法[62]。然而,软组织之间的接触计算不会很好地收敛,特别是当软组织接触表面出现变形时。ATESHIAN等[63]认为FEBio软件可能能够解决这个问题。相关结果表明,除反作用力外,肌力对胫骨和距骨的应力分布也有影响[64]。 在不包括肌肉力量的情况下,胫骨和距骨不同位置的应力减少了10%-50%,特别是在距骨的上部和下部,发现应力减少了10%-40%。不同骨骼和软骨的几何形状是基于单个MRI扫描数据集生成的,这有助于定性地估计形成踝关节的不同骨骼中的载荷转移和应力分布。然而,对于应力分布的定量估计,考虑患者变异性(年龄、性别和体质量)影响的踝关节研究会更好地了解形成踝关节的不同骨骼中的载荷转移和应力分布。 2.2.6 模型验证 通过模型验证对仿真模型的计算结果进行验证,评估有限元计算的可信度。模型验证的数据主要来自生物力学实验或参考文献[65], 有实验验证将使模型更加合理[66]。验证性实验的设计主要根据研究目的和所涉及的变量进行。许多不同的实验方法可以应用在研究中以获得验证数据。动态荧光透视装置可以获得运动中骨结构的位置[67]。体外生物力学装置可以通过记录人体在地面上的载荷和运动轨迹来获得生物力学数据,例如运动学数据[67]。踝关节运动学可以用特定的运动捕捉系统和机械采集设备进行评估,以获得运动学和机械数据[68]。 通过与踝关节的位移、旋转、接触面积和接触压力进行比较,可以验证模型的有效性[69]。通过在韧带中置入压力传感器可以获得应力-应变等局部变量,带有传感器的踝关节假体还可以提供关节表面应力等数据。肌电信号可以作为肌肉模型的客观评估指标[65],将实验数据与有限元预测结果进行线性回归比较,可有效地评价模型的精度[69]。 2.3 临床及康复应用 有限元模型有助于更好地理解疾病 的发病机制,为临床应用和康复训练提供有效的支持。 2.3.1 临床应用 有限元分析广泛用于骨和软骨缺损、骨关节炎、韧带损伤的研究中。使用松质骨移植治疗胫骨假 体下的骨缺损会导致假体上更大的微移动和更高的应力,这可以通过使用更硬的移植材料来改善,如压缩的松质骨 [70]。LIU 等 [71] 比较了金属块和骨水泥螺钉治疗胫骨缺损的结果,发现骨水泥螺钉更兼容,适用于小骨缺陷;金属块更坚固,适合于大面积骨缺损。踝骨关节炎的手术治疗通常包括关节成形术或截骨术。有限元模型可以用来指导临床决策,有学者设计了一种有限元模型,采用有限元仿真的方法,探究距腓前韧带形态学参数与力学属性变化对踝关节稳定性的影响,为踝关节不稳的诊断与治疗提供了生物力学方面的理论基础。 2.3.2 康复训练 有限元分析可为康复训练提供更多的指 导和建议。有研究对骨关节炎患者的日常活动和康复活动进行了有限元分析,在大多数日常活动中发现内侧胫骨比外侧胫骨有更大的机械应力,这一结果与内侧较高的患病率相符合。踝关节有限元模型还可以作为运动和训练的辅助工具,帮助运动员进行更安全的训练,并获得更好的运动成绩。NAVACCHIA 等[58]开发了一种跟踪下肢关节运动的方法,该方法结合有限元模型可以有效地估计肌肉力量和组织变形之间的关系,表明了有限元法在肌肉力量预测中的可行性。 "
| [1] 彭琳晶,王心桐,干耀恺,等.距腓前韧带影响踝关节不稳的生物力学研究[J]. 医用生物力学,2023,38(4):736-741. [2] 杨亦敏,张泽毅,刘卉,等.护踝对功能性踝关节不稳患者下肢运动生物力学特征的影响[J].医用生物力学,2023, 38(4):742-748. [3] 王国栋,毛晓锟,张秋霞,等.功能性踝关节不稳者静态姿势控制中压力中心时域频域特征分析[J].中国运动医学杂志, 2021,40(9): 691-697. [4] 付光亮,孟庆华,鲍春雨.功能性踝关节不稳者本体感觉力学差异及平衡训练干预效果[J].应用力学学报,2021,38(6): 2426-2431. [5] DU M, LI J, JIAO C, et al. Distal insertion rupture of lateral ankle ligament as a predictor of weakened and delayed sports recovery after acute ligament repair: mid-term outcomes of 117 cases. BMC Musculoskelet Disord. 2022; 23(1):294. [6] CAMPBELL KJ, MICHALSKI MP, WILSON KJ, et al. The ligament anatomy of the deltoid complex of the ankle: a qualitative and quantitative anatomical study. J Bone Joint Surg Am. 2014;96(8):e62. [7] KIELY PDW, LLOYD ME. Ankle arthritis - an important signpost in rheumatologic practice. Rheumatology (Oxford). 2021; 60(1):23-33. [8] DODD A, PINSKER E, YOUNGER ASE, et al. Sex Differences in End-Stage Ankle Arthritis and Following Total Ankle Replacement or Ankle Arthrodesis. J Bone Joint Surg Am. 2022;104(3):221-228. [9] TANTIGATE D, NOBACK PC, BACKER HC, et al. Anatomy of the ankle capsule: A cadaveric study. Clin Anat. 2018;31(7):1018-1023. [10] GOSSELIN MM, HAYNES JA, MCCORMICK JJ, et al. The Arterial Anatomy of the Lateral Ligament Complex of the Ankle: A Cadaveric Study. Am J Sports Med. 2019;47(1):138-143. [11] INCHAI C, VASEENON T, TANAKA Y, et al. The Specific Anatomical Morphology of Lateral Ankle Ligament: Qualitative and Quantitative Cadaveric based Study. Orthop Surg. 2023;15(10):2683-2688. [12] PARK S, LEE S, YOON J, et al. Finite element analysis of knee and ankle joint during gait based on motion analysis. Med Eng Phys. 2019;63:33-41. [13] LI J, WANG Y, WEI Y, et al. The effect of talus osteochondral defects of different area size on ankle joint stability: a finite element analysis. BMC Musculoskelet Disord. 2022:23:500. [14] GUNDAPANENI D, TSATALIS JT, LAUGHLIN RT, et al. Wear characteristics of WSU total ankle replacement devices under shear and torsion loads. J Mech Behav Biomed Mater. 2015;44:202-223. [15] CHEN TL, WONG DW, WANG Y, et al. Foot arch deformation and plantar fascia loading during running with rearfoot strike and forefoot strike: A dynamic finite element analysis. J Biomech. 2019;83:260-272. [16] KACHMAR M, PIAZZA SJ, BADER DA. Comparison of growth plate violations for transtibial and anteromedial surgical techniques in simulated adolescent anterior cruciate ligament reconstruction. Am J Sports Med. 2016;44(2):417-424. [17] WU C, WANG X, ZHANG H, et al. Biomechanical analysis of different internal fixation methods for special Maisonneuve fracture of the ankle joint based on finite element analysis. Injury. 2023;54(8):110917. [18] KELLER G, ESTLER A, HERRMANN J, et al. Prospective intraindividual comparison of a standard 2D TSE MRI protocol for ankle imaging and a deep learning-based 2D TSE MRI protocol with a scan time reduction of 48%. Radiol Med. 2023;128:347-356. [19] YIN XY, PARK DY, KIM YJ, et al. The effect of distance between holes on the structural stability of subchondral bone in microfracture surgery: a finite element model study. BMC Musculoskelet Disord. 2020;21(1):557. [20] TANSKA P, VENALAINEN MS, ERDEMIR A, et al. A multiscale framework for evaluating three-dimensional cell mechanics in fibril-reinforced poroelastic tissues with anatomical cell distribution - analysis of chondrocyte deformation behavior in mechanically loaded articular cartilage. J Biomech. 2020;101:109648. [21] LIN W, MENG Q, LI J, et al. The effect of highly inhomogeneous biphasic properties on mechanical behaviour of articular cartilage. Comput Methods Programs Biomed. 2021;206:106122. [22] WARNECKE D, BALKO J, HAAS J, et al. Degeneration alters the biomechanical properties and structural composition of lateral human menisci. Osteoarthr Cartil. 2020;28(11):1482-1491. [23] OZEN M, SAYMAN O, HAVITCIOGLU H. Modelling and stress analyses of a normal foot-ankle and a prosthetic foot-ankle complex. Acta Bioeng Biomech. 2013;15(3):19-27. [24] TAO K, WANG D, WANG C, et al. An in vivo experimental validation of a computational model of human foot. J Bionic Eng. 2009;6:387-397. [25] VENJAKOB E, YAO D, ETTINGER S, et al . Feasibility and reliability of DEXA analysis after total ankle arthroplasty: A cadaver study. Foot Ankle Surg. 2021;27(1):110-115. [26] YU J, CHEUNG JT, FAN Y, et al . Development of a finite element model of female foot for high heeled shoe design. Clin Biomech. 2008;23:31-38. [27] RAMLEE MH, KADIR MRA, HARUN H. Three-dimensional modelling and analysis of a human ankle joint. IEEE Student Conf Res Dev (SCOReD). 2013. [28] GEFEN A, MEGIDO RM, ARCHON M. Biomechanical analysis of three dimensional foot structure during gait: A basic tool for clinical applications. J Biomech Eng. 2000;122:629-639. [29] CHEUNG JTM, ZHANG M, LEUNG AK, et al. Three-dimensional finite element analysis of the foot during standing- a material sensitivity study. J Biomech.2005;38:1045-1054. [30] HSU CY, GUNG WY, SHIH LS. Using an optimization approach to design an insole for lowering plantar fascia stress-A finite element study. Ann Biomech Eng. 2008;36:1345-1352. [31] IAQUINTO JM, WAYNE JS. Computational model of the lower leg and foot/ankle complex: application to arch stability. J Biomech Eng. 2010;132(2):021009-021014. [32] QIU TX, TEO EC, LEI W. Finite element modelling of 3D coupled foot-boot model. Med Eng Phys. 2011;33:1228-1233. [33] GEFEN A, MEGIDO-RAVID M, ITZCHAK Y, et al . Biomechanical analysis of the three-dimensional foot structure during gait: a basic tool for clinical applications. J Biomech Eng. 2000;122(6):630-639. [34] CHEN TL, WONG DW, WANG Y, et al. Foot arch deformation and plantar fascia loading during running with rearfoot strike and forefoot strike: A dynamic finite element analysis. J Biomech. 2019;83:260-272. [35] LI J, WEI Y, WEI M. Finite Element Analysis of the Effect of Talar Osteochondral Defects of Different Depths on Ankle Joint Stability. Med Sci Monit. 2020;26: e921823. [36] SUN D, SONG Y, CEN X, et al. Workflow assessing the effect of Achilles tendon rupture on gait function and metatarsal stress: Combined musculoskeletal modeling and finite element analysis. Proc Inst Mech Eng H. 2022;236(5):676-685. [37] NIU WX. Effects of bone Young’s Modulus on finite element analysis in the lateral ankle biomechanics. Appl Bionics Biomech. 2013;10: 818414. [38] FORESTIERO A, CARNIEL EL, FONTANELLA CG, et al. Numerical model for healthy and injured ankle ligaments. Australas Phys Eng Sci Med. 2017;40(2):289-295. [39] ATESHIAN GA, CHAHINE NO, BASALO IM, et al. The correspondence between equilibrium biphasic and triphasic material properties in mixture models of articular cartilage. J Biomech. 2004; 37(3):391-400. [40] WU JZ, HERZOG W, FEDERICO S. Finite element modeling of finite deformable, biphasic biological tissues with transversely isotropic statistically distributed fibers: toward a practical solution. Z Angew Math Phys. 2016;67:26. [41] HISLOP BD, HEVERAN CM, JUNE RK. Development and analytical validation of a finite element model of fluid transport through osteochondral tissue. J Biomech. 2021;123:110497. [42] KıLıÇASLAN ÖF, LEVENT A, ÇELIK HK, et al. Effect of cartilage thickness mismatch in osteochondral grafting from knee to talus on articular contact pressures: A finite element analysis. Jt Dis Relat Surg. 2021;32(2):355-362. [43] BUTZ KD, CHAN DD, NAUMAN EA, et al. Stress distributions and material properties determined in articular cartilage from MRI-based finite strains. J Biomech. 2011; 44(15):2667-2672. [44] AKRAMI M, QIAN Z, ZOU Z, et al. Subject-specific finite element modelling of the human foot complex during walking: sensitivity analysis of material properties, boundary and loading conditions. Biomech Model Mechanobiol. 2018;17(2):559-576. [45] RAMOS A, ROCHA C, MESNARD M. The effect of osteochondral lesion size and ankle joint position on cartilage behavior - numerical and in vitro experimental results. Med Eng Phys. 2021;98:73-82. [46] FILARDI V. Finite element analysis of the foot: stress and displacement shielding. J Orthop. 2018;15(4):974-979. [47] GUAN M. Finite element analysis of the effect of sagittal angle on ankle joint stability in posterior malleolus fracture: a cohort study. Int J Surg. 2019;70:53-59. [48] CHEN TL, WONG DW, WANG Y, et al. Foot arch deformation and plantar fascia loading during running with rearfoot strike and forefoot strike: a dynamic finite element analysis. J Biomech. 2019;83:260-272. [49] BAE JY, PARK KS, SEON JK, et al. Analysis of the Effects of Normal Walking on Ankle Joint Contact Characteristics After Acute Inversion Ankle Sprain. Ann Biomed Eng. 2015;43(12):3015-3024. [50] NI M, SUN T, ZHANG T, et al. Quantitative initial safety range of early passive rehabilitation after ankle fracture surgery. Injury. 2022;53(6):2281-2286. [51] SUN D, SONG Y, CEN X, et al. Workflow assessing the effect of Achilles tendon rupture on gait function and metatarsal stress: Combined musculoskeletal modeling and finite element analysis. Proc Inst Mech Eng H. 2022;236(5):676-685. [52] ESRAFILIAN A, STENROTH L, MONONEN ME, et al. Toward tailored rehabilitation by implementation of a novel musculoskeletal finite element analysis pipeline. IEEE Trans Neural Syst Rehabil Eng. 2022;30:789-802. [53] SHU L, YAO J, YAMAMOTO K, et al. In vivo kinematical validated knee model for preclinical testing of total knee replacement. Comput Biol Med. 2021; 132:104311. [54] WANG K, HOSSEINNEJAD SH, JABRAN A, et al. A biomechanical analysis of 3D stress and strain patterns in patellar tendon during knee flexion. Int J Numer Method Biomed Eng. 2020;36(9):e3379. [55] BERTON A, SALVATORE G, NAZARIAN A, et al. Combined MPFL reconstruction and tibial tuberosity transfer avoid focal patella overload in the setting of elevated TT-TG distances. Knee Surg Sports Traumatol Arthrosc. 2022;31:1771-1780. [56] HUME DR, RULLKOETTER PJ, SHELBURNE KB. ReadySim: a computational framework for building explicit finite eleme nt musculoskeletal simulations directly from motion laboratory data. Int J Numer Method Biomed Eng. 2020; 36(11):e3396. [57] DELP SL, ANDERSON FC, ARNOLD AS, et al. OpenSim:open-source software to create and analyze dynamic simulation s of movement.IEEE Trans Biomed Eng. 2007;54(11):1940-1950. [58] NAVACCHIA A, HUME DR, RULLKOETTER PJ, et al. A computationally efficient strategy to estimate muscle forces in a finite element musculoskeletal model of the lower limb. J Biomech. 2019;84:94-102. [59] ESRAFILIAN A, STENROTH L, MONONEN ME, et al. An EMG-assisted muscle-force driven finite element analysis pipeline to investigate joint- and tissue-level mechanical responses in functional activities: towards a rapid assessment toolbox. IEEE Trans Biomed Eng. 2022; 69(9):2860-2871. [60] RADIN EL, PAUL IL. A consolidated concept of joint lubrication. J Bone Joint Surg Am. 1972;54(3):607-613. [61] FARROKHI S, KEYAK JH, POWERS CM. Individuals with patellofemoral pain exhibit greater patellofemoral joint stress: a finite element analysis study. Osteoarthr Cartil. 2011;19(3):287-294. [62] BEHRENS BA, DRÖDER K, HÜRKAMP A, et al. Finite element and finite volume modelling of friction drilling HSLA steel under experimental comparison. Materials (Basel). 2021;14(20):5997. [63] ATESHIAN GA, MAAS S, WEISS JA. Finite element algorithm for frictionless contact of porous permeable media under finite deformation and sliding.J Biomech Eng. 2010;132(6):61006. [64] MONDAL S, GHOSH R. A numerical study on stress distribution across the ankle joint: Effects of material distribution of bone, muscle force and ligaments. J Orthop. 2017; 14(3): 329-335. [65] NAVACCHIA A, HUME DR, RULLKOETTER PJ, et al. A computationally efficient strategy to estimate muscle forces in a finite element musculoskeletal model of the lower limb. J Biomech. 2019;84:94-102. [66] HENNINGER HB, REESE SP, ANDERSON AE, et al. Validation of computational models in biomechanics. Proc Inst Mech Eng H. 2010;224(7):801-812. [67] SHU L, YAO J, YAMAMOTO K, SATO T,et al. In vivo kinematical validated knee model for preclinical testing of total knee replacement. Comput Biol Med. 2021;132:104311. [68] GUAN M, ZHAO J, KUANG Y, et al. Finite element analysis of the effect of sagittal angle on ankle joint stability in posterior malleolus fracture: A cohort study. Int J Surg. 2019;70:53-59. [69] GRASSI L, SCHILEO E, TADDEI F, et al. Accuracy of finite element predictions in sideways load configurations for the proximal human femur. J Biomech. 2012; 45(2):394-399. [70] TOTORIBE K, CHOSA E, YAMAKO G, et al. Finite element analysis of the tibial bone graft in cementless total knee arthroplasty. J Orthop Surg Res. 2018;13(1):113. [71] LIU Y, ZHANG A, WANG C. Biomechanical comparison between metal block and cement-screw techniques for the treatment of tibial bone defects in total knee arthroplasty based on finite element analysis. Comput Biol Med. 2020; 125:104006. |
| [1] | Chen Qiuhan, Yang Long, Yuan Daizhu, Wu Zhanyu, Zou Zihao, Ye Chuan. Peri-knee osteotomy for treatment of knee osteoarthritis: optimization of treatment strategies [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2303-2312. |
| [2] | Zhang Zizheng, Luo Wang, Liu Changlu. Application value of finite element analysis on unicompartmental knee arthroplasty for medial knee compartmental osteoarthritis [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2313-2322. |
| [3] | Zhang Xianxu, Ma Zhong, Liu Xin, Huang Lei, Shen Wenxiang, Luo Zhiqiang . Lumbar fusion combined with unilateral fixation for lumbar degenerative diseases: biomechanics, technical evolution, and clinical applications [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2334-2342. |
| [4] | Chen Huiting, Zeng Weiquan, Zhou Jianhong, Wang Jie, Zhuang Congying, Chen Peiyou, Liang Zeqian, Deng Weiming. Tail anchoring technique of vertebroplasty in treatment of osteoporotic vertebral compression fractures with intravertebral cleft: a finite element analysis [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2145-2152. |
| [5] | Zeng Xuan, Weng Rui, Ye Shicheng, Tang Jiadong, Mo Ling, Li Wenchao. Two lumbar rotary manipulation techniques in treating lumbar disc herniation: a finite element analysis of biomechanical differences [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2153-2161. |
| [6] | Cheng Qisheng, Julaiti·Maitirouzi, Xiao Yang, Zhang Chenwei, Paerhati·Rexiti. Finite element analysis of novel variable-diameter screws in modified cortical bone trajectory of lumbar vertebrae [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2162-2171. |
| [7] | Wu Hongxu, Liu Xuanyu, Wang Taoyu, Wang Shiyao, Cheng Jingyi, Zhang Mingwen, Zhang Yinxia, Liu Zhihua, Wang Xiaojie. Finite element simulation of scoliosis with muscle unit introduction: verification of correction effect under bidirectional load [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2172-2181. |
| [8] | Liu Jiafu, Ren Ruxia, Liao Zhouwei, Zhou Xiali, Wu Yihong, Zhang Shaoqun. Three-dimensional finite element analysis of cervical spine biomechanical characteristics in a rat model of cervical vertigo [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2182-2190. |
| [9] | Liu Wenlong, Dong Lei, Xiao Zhengzheng, Nie Yu. Finite element analysis of tibial prosthesis loosening after fixed-bearing unicompartmental knee arthroplasty for osteoporosis [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2191-2198. |
| [10] | Zheng Wangyang, Fei Ji, Yang Di, Zhao Lang, Wang Lingli, Liu Peng, Li Haiyang. Finite element analysis of the force changes of the supraspinatus tendon and glenohumeral joint during the abduction and flexion of the humerus [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2199-2207. |
| [11] | Cai Qirui, Dai Xiaowei, Zheng Xiaobin, Jian Sili, Lu Shaoping, Liu Texi, Liu Guoke, Lin Yuanfang. Mechanical effects of Long’s traction orthopedic method on cervical functional units: quantitative analysis of biomechanical model of head and neck [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2208-2216. |
| [12] | Rao Jingcheng, Li Yuwan, Zheng Hongbing, Xu Zhi, Zhu Aixiang, Shi Ce, Wang Bing, Yang Chun, Kong Xiangru, Zhu Dawei. Biomechanical differences between the new proximal femoral stable intramedullary nail and traditional intramedullary nail#br# [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2217-2225. |
| [13] | Chen Long, Wang Xiaozhen, Xi Jintao, Lu Qilin. Biomechanical performance of short-segment screw fixation combined with expandable polyetheretherketone vertebral body replacement in osteoporotic vertebrae [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2226-2235. |
| [14] | Yan Xiangning, Chen Lei, Chen Yonghuan, Wang Chao, Li Xiaosheng. Influence of different depths and loads on knee joint mechanics and peripheral muscle force characteristics during squatting [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2236-2247. |
| [15] | Zhou Daobin, Wang Kehao, Xie Yang, Ning Rende. Biomechanical characteristics of volar locking plate only versus combined dorsal mini-plate fixation of distal radius fractures with dorsal ulnar fragment [J]. Chinese Journal of Tissue Engineering Research, 2026, 30(9): 2255-2261. |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||