Chinese Journal of Tissue Engineering Research ›› 2022, Vol. 26 ›› Issue (20): 3256-3264.doi: 10.12307/2022.630
Previous Articles Next Articles
Motor coordination: evolution of theoretical model and quantitative method
Wang Jiawei, Liu Ye
- Beijing Sport University, Beijing 100084, China
-
Received:2021-07-06Revised:2021-07-08Accepted:2021-08-19Online:2022-07-18Published:2022-01-20 -
Contact:Liu Ye, PhD, Professor, Beijing Sport University, Beijing 100084, China -
About author:Wang Jiawei, Master candidate, Beijing Sport University, Beijing 100084, China -
Supported by:the Scientific Fitness Instruction Project of the General Administration of Sports of China, No. 2017B022 (to LY); a grant from the Key Laboratory of "Sports and Physical Health" of the Ministry of Education of China
CLC Number:
Cite this article
Wang Jiawei, Liu Ye. Motor coordination: evolution of theoretical model and quantitative method[J]. Chinese Journal of Tissue Engineering Research, 2022, 26(20): 3256-3264.
share this article
Add to citation manager EndNote|Reference Manager|ProCite|BibTeX|RefWorks

2.1.1 肌肉协调理论模型演进 以往研究观察到基于肌肉结构化控制的假设[11-12],其变异组合负责几种肌肉模式和复杂的运动行为[13]。因此,通过运动的结构化(即少量肌肉在运动中的协同作用),中枢神经系统可以通过使用几个组合系数有效地将高维数据减少到低维元素[13]。在过去几十年里,已经提出了几个结构化控制的理论模型,例如,神经运动协同[14]、脊柱力场[15]、反射以及肌肉协同[16-18]。其中,大部分理论模型面临的挑战在于确定这些假设结构的存在,以及它们构建运动行为所发挥的作用。具体来说,大部分证据来自脊髓或去脑化实验,而许多实验缺乏完整动物与环境相互作用以实现目标行为所特有的复杂性和变异性[11],但关于肌肉协同的实验证据已经在蛙[18]、猴子和健康人中得到验证[19-20]。 (1)肌肉协同假说(muscle synergy hypothesis)来源于对自由度和运动等效性问题的解决。该假说认为,人体是一个非常复杂的多环节系统,每个环节具有一个或多个自由度。在生物力学系统中,可以通过形成协调结构来减少自由度的个数,这种同步激活的协调结构被定义为满足任务需求的前提下跨多个关节的肌肉协同[21],中枢神经系统正是通过利用协同减少控制参数,以简化对人体运动的控制。它将运动指令传递给中枢模式发生器(Central Pattern Generator),通过控制协同结构从而实现运动协调[22]。间接证据表明,肌肉协同作用存在于脑干和(或)脊髓,遵循结构化组织[23]。肌肉协同作用被认为是低维单位,它为一组肌肉产生复杂的激活模式,可以在任务执行过程中通过肌电图记录[24]。协同作用可以在大脑皮质或脊髓水平上观察到[25-26],表明在中枢神经系统的结构层次中有高度的配合[27],这种控制方式被称为分层控制方式,也被称为M-模式[28]。中枢神经系统对少数运动协调元的控制处于高层次的控制,运动协调元对运动器官的控制处于低层次的控制[29],但这种协调并不会完全消除系统的变异性。了解肌肉协同作用有助于阐明许多神经疾病的机制,包括脑瘫[30]、脊髓损伤和帕金森病等[31-32]。 另外,肌肉协同结构可能在各种活动中共享,意味着如果2个不同的运动任务包括一个共同的子任务,则在2个协同组中可能出现共同的肌肉协同[33]。此外,感觉反馈有助于调节肌肉协同,使运动输出适应外部环境[34]。 (2)平衡点假说(equilibrium-point hypothesis,EPH)也称“阈值控制理论”,因为该假说认为从中枢神经系统发送到外周的信号被认为是调节每个肌肉的阈值长度。平衡点假说起源于FELDMAN[35-36]对人体肘关节3种动作的比较试验,这3种动作分别为:手臂卸荷时引起的非自主运动(卸荷反射)、有意改变关节角度的运动以及当受试者放松手臂肌肉时他人移动受试者手臂的被动运动。试验目的是确定保持不变或被修改以进行这些动作的神经生理学变量,卸荷反射是通过让受试者在矢状面上屈肘时对抗重力,同时在手掌上握住一本厚重的书来证明的,当助手突然拿起书时,手臂会不自觉地向上移动,而后停在某个屈曲位。这样的反应不需要指令,但取决于受试者在非自愿干预阶段及时卸荷的能力[37]。该假说早期是为单一肌肉和单关节系统开发的,后来的研究将该模型推广到多关节[38]、全身姿势以及运动控制[39]。 平衡点假说基于伽利略的相对论和神经元是阈值元素的事实[10],是运动控制领域中唯一将中枢神经系统使用的生理变量指定为控制变量的理论[36]。该假说认为,运动神经元向肌肉发送命令,改变力-长度关系,导致系统平衡点的变化,神经系统不需要直接估计肢体动力学,但肌肉和脊髓的反射会提供有关系统状态的所有必要信息[40],因为控制神经系统水平实际上并不能解决冗余问题,它们只是限制了不同自由度之间可能的协调,而冗余问题的解决方案是通过神经肌肉元素之间,以及这些元素与环境之间的实际相互作用实现的[41]。具体而言,中枢控制信号将α运动神经元的激活阈值改变为通过阈下α运动神经元去极化与肌肉长度(紧张性牵张反射阈值,λ)相关的传入信号,中枢信号并不是唯一影响λ的因素,它还会随着肌肉收缩速度(因为肌梭末端的速度敏感性)、其它肌肉的感受器信号和激活史而改变[42]。换言之,动作是由神经系统引导的,神经系统通过指定神经肌肉元素所处的位置,而不是指定需要哪些元素及如何工作来控制动作。因此,不需担心任何神经层面的冗余问题[36]。并且,当平衡状态受到干扰时,机体将会激发相应运动行为予以应对,从而维持平衡状态[29]。 平衡点假说提出至今已近60年,期间争议不断。许多批评者认为该假说有许多未解决的局限性,比如在运动中测量的肌肉对抗位移时的阻力(通常被称为肌肉刚度)是否大到足以支持这种形式的控制[43],同时认为该假说在很大程度上仍是一种推测,不能作为一种“科学理论”[44]。相反,支持者认为,该假说是唯一连贯地利用生理学解释运动神经控制的物理定律[28],无须费时证明或反驳这一假设,而应发展该假说,包括应用到复杂肌肉运动的分析,将其与感知相联系等[45]。但关于该假说,有3点结论得到了所有学者的支持,包括:①神经元是阈值元素;②肌肉的自主激活与相应的α运动神经元池激活阈值的变化有关;③肌肉激活水平(和所有机械变量)是相应脊椎节段的下行信号和影响外周感受器输入的外力场共同作用的结果[8]。 (3)对照设置假说(Referent configuration hypothesis)是平衡点假说的发展。FELDMAN[36]在模拟预期握力增加的手臂运动时,使用了一种应用于多个骨骼肌和关节的特定形式的阈值位置控制,这种控制是通过身体或其部分参照物结构的变化来实现的。对照设置假说代表神经控制行为的物理方法,可以与协同的分层控制方式相结合[45]。 该假说认为,中枢神经系统给人体建立了一个对照设置(referent configuration,简称RC,或称参数值),这种预设的参数值会给人体提供一个姿势的平衡位置参数,如果身体的实际姿势与中枢神经系统设定的参数值一致,则不会观察到肌肉的激活;如果身体发生偏移,则控制姿势的肌肉会根据预设参数值进行调整,回到平衡点[46]。通常,由于解剖学和外力的限制,实际形态不能达到中枢神经系统预先设定的参数,从而导致平衡时的肌肉激活水平不为零[42]。换句话说,神经系统并不计算关于运动的众多变量(如肌肉力量、关节角度、肢体轨迹等);相反,它只是将肢体的平衡(参数值)构形转移到一个新的位置(或改变伸展反射肌肉长度阈值),并且由于反射诱发的肌肉活动,肢体移动到新的构形。而在预先给定参数值的情况下,神经肌肉系统会试图达到肌肉最小激活的状态,这一基本原则可以称为最小最终行动原则(The principle of minimal final action),该原则被定为对照设置假说的指导原则,它与最小交互原则相近。最小交互原则认为,系统依赖于神经肌肉元件自身的能力进行相互作用,并与环境相互作用,将受限的集合减少到一个独特的动作,从而解决运动控制中的冗余问题[47]。 目前,关于平衡点假说(含对照设置假说)定义的阈值位置控制效率已在几个单关节和多关节手臂运动的模拟中多次得到证明,阈值位置控制也被用来分析和模拟诸如适应、预判和学习等运动行为[48],并且有大量的实验证据和坚实的物理学和神经生理学基础[49]。另外,平衡点假说已得到许多应用,包括对神经科患者运动障碍的研究[45],该假说能够帮助理解中枢神经系统受到损伤的患者表现出的运动控制不足,进而通过改善紧张性牵张反射的阈值,提高患者的运动能力[50]。 2.1.2 肢体协调理论模型演进 肢体协调又称为关节协调,其特点之一是存在变异性。在肌肉协调中,协同是对自由度的组织,而冗余自由度被认为是产生变异性的主要原因。协同将冗余自由度组织成一个控制单元,但由于肌肉骨骼和神经运动系统的冗余性,不同协调模式或协调模式的微小变化可用于完成相同的任务,导致协调变异性。协调变异性问题最早源于BERNSTEIN[2]观察铁匠每次锤击的落点相同,轨迹不同的实验,称之为“重复而不重复”,见图5,即一个行为的每次重复都涉及独特的、非重复的神经和运动模式。如果一个人试图重复同一动作2次,那么2个动作永远不会完全相同,即系统的变异性一直存在,这表明变异性不仅仅是随机误差,也可能存在于控制系统本身。"


过去,在生物力学和运动控制领域等大多数研究中,变异性等同于噪声,与运动表现下降和病理学表现相联系,通常作为误差源从数据中消除,但现在人们提出了许多理论模型试图了解协调变异性的特点。 (1)动作图式理论。图式理论起源于神经学[51],而动作图式理论则是通过SCHMIDT[52]的研究正式提出,该理论认为,动作程序不是特定的肌肉指令,而是抽象的、以记忆为基础的一类动作的表征,其每一类动作都有固定特征,学习者为能够阐述与情景环境要求相适应的协调运动,必须从记忆中提取适宜这类动作的一般运动程序特征(固有特征),再添加特定的可变参数以实现该运动。基于当时闭环控制理论解释慢速动作的局限以及动作程序理论的容量问题,它提供了一个更经济的解释,说明人类能够执行的众多运动变化是如何产生和存储的。这种能力背后的记忆表征是一般运动程序(generalized motor program,GMP)和动作图式(schema)[53],动作图式可以理解为运动情景的具体特征,为GMP提供参数,GMP结合动作图式即可实际执行动作技能,图式的多样性意味着动作表现的多样性。该理论的一个重要主张是它处理了2个运动学习问题:第一个是学习的新颖性问题,即一个人如何学习以前没有完成过的运动任务;第二个问题是运动记忆存储问题,它认为人类中枢神经系统的记忆容量不足以储存一生中所有活动需要的运动特征。因此,动作图式理论中的学习是建立在更丰富的运动程序发展基础上,即随着学习的推进,个人会发展出广泛的与同类任务相关的运动技能来处理日常活动需求[54]。该理论可以用于解释人体如何完成一项从未进行过的技能,其中练习的变异性有助于动作技能学习。 动作图式理论最初提出是针对运动行为学习,而此后广泛引用到其他学科,包括认知心理学、神经科学、音乐感知、人体工程学等领域[53,55-56]。但该理论近年的发展,也表露了局限性,批评者认为它的假设过于简单化,无法解释更复杂的学习情况,并且该理论在提出时只是假设GMP的存在,并没有提供发展GMP的机制或过程[53]。另外,由于过于广泛的应用,批评者认为此理论没有统一连贯的整体[57]。同时,由于协调结构理论(coordinative structure theory)和动态系统框架(dynamical systems framework)的相继提出[58],对运动协调也形成了新的解释。 (2)动态系统理论(dynamic systems theory)。在运动控制领域,动态系统理论由协调结构理论发展而来,与此前的运动程序或动作图式等理论不同的是,传统的运动程序理论倾向于强调中枢神经的控制地位,但在研究中找不到对应的实体结构,而且倾向于自上而下的控制方式和唯一解。而动态系统理论认为,运动不完全由中枢神经系统决定,需要考虑其它限制性因素,由此确立了3种约束:个人约束、环境约束和任务约束。从20世纪80年代始,KUGLER等[59]就意识到协调结构理论更多强调的是动态规律,而非运动的既定规则,而与动态系统理论相比,动作图式理论更多是一种静态的学习理论[54]。 动态系统理论认为,生物系统的功能并不是内部元素的简单相加,也非自上而下的组织方式,而是根据环境、生物力学和形态学的约束进行自组织,以找到产生给定运动的最稳定的解决方案[21]。因此,该理论将运动协调视为运动器官各元素之间稳定的、重复性高的相互间关系[60]。除了稳定性以外,灵活性也是动态系统的重要概念,而变异性作为动态系统的固有特性[61],同样是反映灵活性的重要指标,对人类运动起着重要的功能作用[62]。但在运动模式中,变异性的增加通常被认为是稳定性的丧失,变异性降低通常表明行为高度稳定。所以在早期的讨论中,变异性被认为是系统的缺陷或误差[63]。当变异性增加并达到特定临界点时,系统变得高度不稳定,并切换到新的、更稳定的运动模式,由此带来的转变,使得人体不断打破既有平衡维持新的稳态,具有明显的非线性特征。所以传统的统计工具只可以量化一组值的变化幅度,而不考虑它们在分布中的顺序,这对于线性系统是合适的,而研究非线性动态系统的工具,则需要能够捕捉运动行为随时间的变化。 (3)非控制流形假说(Uncontrolled manifold hypothesis)。传统观点认为,冗余自由度的处理有“限制”(eliminations)、“最优化”(optimization)、“协同”(synergy),这3种方法有一个共同的特点:认为大量自由度的存在是中枢神经系统计算问题的根源,而非控制流形假说则认为:众多的自由度之间不仅能够共享,而且对于丰富的冗余系统,中枢神经系统能将其作为“奢侈物”加以利用,而非限制或消除[64],非控制流形假说最早由SCHOLZ等[65]提出,后续在讨论运动冗余与变异性关系的理论背景下发展,它为理解协同效应提供了一套新的工具和概念,用于分析与潜在重要性能变量的稳定相关的冗余元素集合内的协同变化[8]。在动态系统理论中,运动过程存在多种多样的协调策略,因此协调运动具有灵活性,而协调变异性是反映这种灵活性的重要指标,并可以用来推断神经肌肉系统产生所需运动结果的健康状况。然而太多的变异性会导致稳定性下降,所以,在动态系统中,灵活性和稳定性并不共存,但非控制流形假说基于动态系统方法,巧妙地将稳定性和灵活性结合了起来,认为自由度的利用可以确保运动任务的灵活和稳定,而变异性被视为生物行为灵活性和适应性的先决条件[66]。 非控制流形假说认为神经控制器组织动作的方式是:基本变量空间中的不同方向(由所选分析级别的冗余元素集产生)反映不同的稳定性,这些稳定性来自人移动中的任务和/或意图[28]。例如,假设有3位实验对象被要求用2个手指(拇指和食指)快速按下2个力传感器来产生40 N的总峰值力。显然,这是一个冗余系统,因为有无限的组合(F食指+F拇指)可以满足任务要求:F合力40 N=F食指力+F拇指力[67]。这种组合可分为3种类型:①F较大的食指力+F较小的拇指力=F合力40 N;②F较小的食指力+ F较大的拇指力= F合力40 N;③F均衡的食指力+F均衡的拇指力=F合力40 N。类型③说明两指的力贡献率相当,表示运动任务的完美执行;类型①与②说明如果一个手指产生的力大于其平均贡献,那么另一个手指产生的力就可能减小。 在非控制流形假说中,非控制流形的计算是通过观察重复实验中系统轨迹的自然变异性来实现[65]。所有的假设都在位形空间内进行,其中,基本变量定义为多元素系统的表面元素产生的变量,它取决于如何识别元素以及选择与特定任务相关的变量,在以上例子中,基本变量为单个手指产生的力和力矩;性能变量用来描述一个多元生物系统的整体输出的一个特定特征,它可能会在一组任务中发挥重要作用,在上述例子中,物体上产生的总握力、合力与合力矩可视为性能变量。另外,虚线为非控制流形,沿虚线的变异性不影响运动任务执行(VUCM,即Vgood,也称为“好的变异性”),与非控制流形正交的变异性影响运动任务执行(VORT,即VBAD,也称为“差的变异性”),即非控制流形空间的运动对性能变量不产生影响,ORT空间的运动对性能变量产生影响[65]。 值得一提的是,近年有许多研究将不同理论模型进行整合研究,例如将平衡点假说(对照设置假说)与非控制流形假说相结合成一种单一的运动控制理论进行分析,已取得良好的应用效果[68]。 2.2 运动协调量化方法的演进"


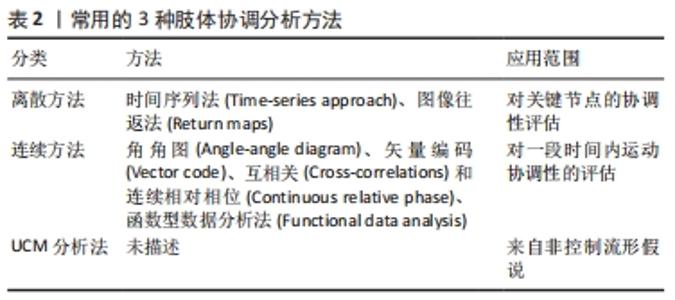
2.2.1 肌肉协同分析 人类行为是中枢神经系统、本体感受器和肌肉之间进行复杂神经动力学运算的结果,目前仍不完全知晓中枢神经系统如何在运动过程中协调大量肌肉的活动。由于人体肌肉骨骼系统的冗余性,中枢神经系统可以从无限多种行为选项中选择最有效的运动方案[2],因此,许多研究试图通过引入运动控制的最佳参数来阐明中枢神经系统和肌肉控制之间的计算机制[69],其中应用最广泛的是肌肉协同分析[11,70-71]。肌肉协同分析的理论基础为肌肉协同假说,其分析方法的核心是将肌电信号(EMG)数据的维数,即肌肉的数量,减少到一组有限变量,称为协同效应,具体方式是根据肌电信号提取协同元和激活系数[72],肌肉协同模型分为时间型、同步型、时变型和统一型4种[73],时间型协同模型中肌肉激活系数不随时间变化,同步性肌肉协同模型中肌肉同时激活,且水平不变,二者模型相似,可以表示为:"

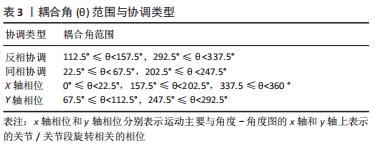
以上4种分解方法都使用二阶或高阶统计量来估计肌肉激活模式的肌肉协同作用,另外,使用时须将肌电信号幅度归一化、基线噪声去除或肌电信号滤波,可能会降低或提高肌电信号的信噪比,并可能对协同效应估计产生影响[92]。而近年采用的极限学习机(Extreme learning machines)是一种相对较新的基于神经网络的学习算法[93],最早应用在行为识别、情感识别和故障诊断等方面,该算法的核心思想是随机选取网络的输入权值和隐式偏置,在训练过程中保持不变,仅需要优化隐藏神经元个数。网络的输出权值则是通过最小化平方损失函数,来求解广义逆矩阵(Moore-Penrose)得到最小范数最小二乘解[94]。此外,还有二阶盲辨识(Second order blind identification),该算法利用时延协方差矩阵的联合对角化来估计未知分量,它可以提供更多的关于肌电活动时间分布的信息,可以体现那些时间延迟上不相关的分量,因此,它有时被认为是基于高阶统计量的独立成分分析的替代[95]。 目前在运动科学领域,使用频率最高的依次为非负矩阵分解、主成分分析、独立成分分析、因子分析、极限学习机和二阶盲辨识。其中,非负矩阵分解法被认为是目前提取行走和跑步中肌肉协同作用的最合适方法[82]。通过肌肉协同分析方法,可识别多个肌肉激活的空间、时间或时空模式的规律性,除了运动科学领域外,已广泛应用于如神经科学、机器人学、医学与康复学等领域[92]。 2.2.2 肢体协调分析 变异性可以反映噪声和潜在的损伤风险,也能反映出一个稳定而适应性强的系统,该系统有效地使用冗余自由度来使运动策略适应预期的运动表现[96]。因此,有些变异性可以提供一定的灵活性来适应不断变化的环境[5]。在运动员多年训练过程中,随着个人获得运动技能方面的专业知识,他们可能会形成一种协调模式,这种模式可以优化运动表现,并保持一定程度的变异性,使其适应不断变化的环境要求或内部限制。例如,肢体协调的变异性可能在短跑表现中起重要作用,因为风速、跑道表面和疲劳等变量的细微变化要求运动员具有一定的适应性。这种变异性增加的第二个好处是载荷在肌肉骨骼组织中的分布或特定组织的累积载荷减少,可以防止过度使用导致的损伤。目前,有许多分析方法量化运动的协调模式和变异性,见表2。"

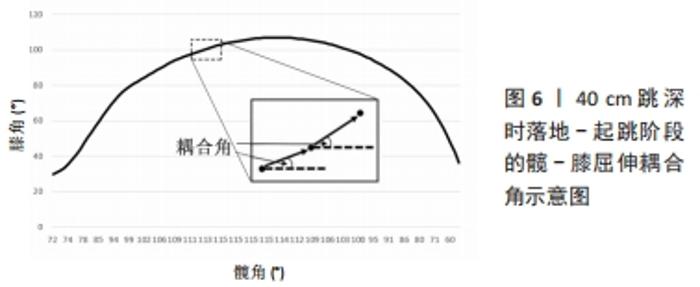
(1)离散方法。运动中的耦合是指关节之间的相互作用,意味着一个关节的运动可以影响另一个关节的运动,比如距下关节外翻的运动必须伴有胫骨内旋和股骨外旋。时间序列法(又称为离散相对相位法)说明了特定耦合中的时间相位关系,使用2个关节角度或2个其它相关生理参数的时间序列,在运动周期的离散事件中确定离散相对相位角。在计算多个步长的平均离散相对相位角以及变异性时,应使用循环统计[97]。 另一个研究运动协调的离散方法是图像往返法,从数值上来说,图像往返法是一个方程的迭代,它将一个点与另一个特定的时间滞后点绘制出来。KELSO等[98]通过计算肢体间的离散相对相位并将其绘制在具有不同滞后点的返回图上,识别出人类多肢体协调中的几个频率比和相位吸引点,目前多应用于运动-呼吸耦合的协调量化,离散方法的缺点是只关注每个运动周期的一个时间节点,无法分析一段时间内的运动;优点是对多个频率比较为敏感性,可用于研究频率比非1∶1的运动系统,例如运动-呼吸耦合。 (2)连续方法。连续方法的理论基础主要来源于动态系统。其中,角角图可用于描述肢体协调模式。该图将2个关节的相对运动表示分别绘制在X、Y轴上,可消除个体或实验之间时域变化的影响。GRIEVE等[99]最早提出将2个关节的角度时间序列相互对立地绘制在相对运动图上。 角角图的优点是可用于协调模式的描述、定性和评估[100],并且直观易懂;缺点是无法量化协调,不适合定量分析[101]。所以,相对运动作为协调性的一种度量,可以用角角图来评估,而用矢量编码方法进行量化[102]。矢量编码用于量化两对关节的协调模式(又称为关节耦合),其中耦合角提供了关于角角图轨迹形状以及肢体间耦合的信息,由连接角角图上两个相邻数据点的矢量与水平轴形成的角度确定,例如图6所示,为40 cm跳深时落地-起跳阶段的髋-膝屈伸耦合角。"
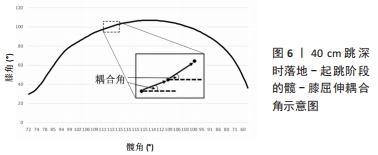

矢量编码分析法的优点是不需要归一化,它比相对相位等复杂技术更直观、更易联系。缺点其一是常用的矢量编码方法涉及计算耦合角,这是一个圆形变量,需要在进一步分析数据时使用方向统计[104];其二是它只提供空间信息,而不考虑时间信息[97]。 此外,互相关分析法是另一种量化角角图差异的常用方法,能量化2个关节角度的时间序列变量间的关系[105]。该方法假设被分析的两个时间序列之间存在线性关系——例如步态期间的髋和膝关节屈曲—伸展角度。然而,与其它方法不同,互相关分析法并不假设变量在运动过程中同步变化[106]。除了确定时间序列之间的关系强度或联系程度之外,互相关分析还揭示了关系的类型(时间序列同相或反相的程度)。该分析法的优点:身体部位和关节的协调动作经常相对于彼此发生时移,因此该方法被认为特别适合于研究人类运动;缺点是不适合具有非线性关系的两时间序列的分析[104]。 最后一种量化角角图中的差异是函数型数据分析法,该方法通过将两关节数据表示为一个唯一函数,将数据分组表示为一个函数族,为角角图的统计分析提供了另一种有效的方法。具体公式如下:"

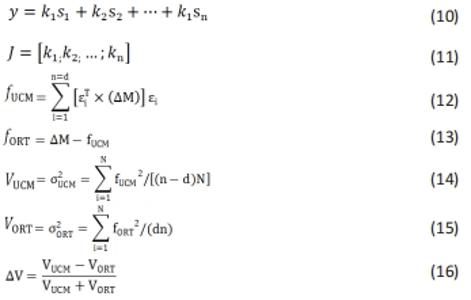
CRP(t)值的范围可以从0-360。然而,角度存在冗余(即,0°和360°表示相同值),因此,比例通常从0°-180°。值接近0°的意味着两个关节同相发展,接近180°或-180°的则是反相发展,负值表示近端关节超前于远端关节,反之亦然[21]。关于角度和角速度的归一化,只有在计算肢体内协调(即同侧肢体,如右侧膝-踝协调)时,才需要数据的归一化,而在计算肢体间协调(非同侧关节)时,不需要进行数据归一化。由于速度被包括在相位角的计算中,连续相对相位提供了对运动协调丰富而详细的分析潜力[97]。 (3)UCM分析法。UCM分析法源于非控制流形假说,已被用于研究各类人群在不同运动任务中站立姿势的稳定性[109]。在这项研究方法中,激活水平成比例缩放的协同活动肌群被定义为肌肉模式(M-Modes)。以M-modes为基本变量,对保持COP坐标的协同指数进行了量化。由前人研究可知[29],UCM的应用步骤有:首先是建立运动器官活动参数与重要任务变量参数之间的联系,有2种方法,一种是应用它们几何位置的关联建立联系,另一种是采用多元回归的方法建立其线性关系[公式(10)]。随后,计算这些方程的雅克比矩阵[公式(11)],求解其零空间的特征值。然后求出所有运动协调元活动系数离均差(?M)在该矩阵零空间及其正交空间的投影[公式(12) (13)]。最后计算零空间及其正交空间投影的方差[公式(14) (15)]以及功能变异性的比率(?V)[公式(16)]。"
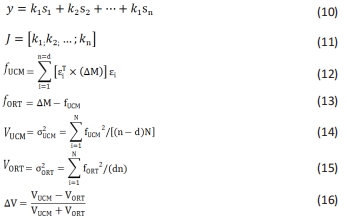
| [1] FREITAS D L, LAUSEN B, MAIA J A, et al. Skeletal Maturation, Body Size, and Motor Coordination in Youth 11-14 Years. Med Sci Sports Exerc. 2016;48(6):1129-1135. [2] BERNSTEIN NA. The co-ordination and regulation of movements. London: Oxford: Pergamon Press, 1967. [3] NEILSON PD, HOSP PH, NEILSON MD, et al. What limits high speed tracking performance? Hum Mov Sci. 1993;12(1-2): 85-109. [4] NEILSON PD, NEILSON MD, O’DWYER NJ. Motor Control and Sensory Motor Integration - Issues and Directions Volume 111 II Chapter 5 Adaptive optimal control of human tracking. Adv Exp Soc Psychol. 1995;111:97-140. [5] VAN EMMERIK REA, ROSENSTEIN MT, MCDERMOTT W J, et al. A Nonlinear Dynamics Approach to Human Movement. J Appl Biomech. 2004;20(4):396-420. [6] LASHLEY KS. Basic neural mechanisms in behavior. Psychol Rev. 1930;37(1):1-24. [7] CISEK P. Neural representations of motor plans, desired trajectories, and controlled objects. Cogn Process. 2005;6(1):15-24. [8] LATASH ML. Two Archetypes of Motor Control Research. Motor Control. 2010; 14(3):e41-e53. [9] WONG AL, HAITH AM, KRAKAUER JW. Motor Planning. Neuroscientist. 2015;21(4): 385-398. [10] LATASH ML, LEVIN MF, SCHOLZ JP, et al. Motor control theories and their applications. Med Lith. 2010;46(6):382-392. [11] D’AVELLA A, SALTIEL P, BIZZI E. Combinations of muscle synergies in the construction of a natural motor behavior. Nat Neurosci. 2003;6(3):300-308. [12] TING LH, MACPHERSON JM. A limited set of muscle synergies for force control during a postural task. J Neurophysiol. 2005;93(1):609-613. [13] D’AVELLA A. Modularity for Motor Control and Motor Learning. Adv Exp Med Biol. 2016;957:3-19. [14] LEE WA. Neuromotor synergies as a basis for coordinated intentional action. J Mot Behav. 1984;16(2): 135-170. [15] BIZZI E, MUSSA-IVALDI F A, GISZTER S. Computations underlying the execution of movement: a biological perspective. Science. 1991;253(5017):287-291. [16] SHERRINGTON C. The Integrative Action of the Nervous System. Nature. 1947; 160(4071):623-624. [17] TRESCH M C, SALTIEL P, BIZZI E. The construction of movement by the spinal cord. Nat Neurosci. 1999;2(2):162-167. [18] SALTIEL P, WYLER-DUDA K, D’AVELLA A, et al. Muscle Synergies Encoded Within the Spinal Cord Evidence From Focal Intraspin. J Neurophysiol. 2001;85(2):605-619. [19] OVERDUIN SA, D’AVELLA A, CARMENA JM, et al. Microstimulation activates a handful of muscle synergies. Neuron. 2012;76(6):1071-1077. [20] D’AVELLA A, PORTONE A, LACQUANITI F. Superposition and modulation of muscle synergies for reaching in response to a change in target location. J Neurophysiol. 2011;106(6):2796-2812. [21] HAMILL J, VAN EMMERIK RE, HEIDERSCHEIT BC, et al. A dynamical systems approach to lower extremity running injuries. Clin Biomech (Bristol, Avon). 1999;14(5):297-308. [22] ANNESHUMWAY-COOK, MARJORIEH. WOOLLACOTT. 运动控制原理与实践 [M]. 毕胜,燕铁斌,王宁华,译.3版.北京:人民卫生出版社, 2009. [23] ROH J, CHEUNG VC, BIZZI E. Modules in the brain stem and spinal cord underlying motor behaviors. J Neurophysiol. 2011;106(3):1363-1378. [24] BIZZI E, CHEUNG VC. The neural origin of muscle synergies. Front Comput Neurosci. 2013;7:51. [25] OVERDUIN SA, D’AVELLA A, ROH J, et al. Representation of Muscle Synergies in the Primate Brain. J Neurosci. 2015;35(37):12615-12624. [26] IVANENKO YP, POPPELE RE, LACQUANITI F. Spinal cord maps of spatiotemporal alpha-motoneuron activation in humans walking at different speeds. J Neurophysiol. 2006;95(2):602-618. [27] SANTUZ A, EKIZOS A, JANSHEN L, et al. Modular Control of Human Movement During Running: An Open Access Data Set. Front Physiol. 2018; 9:1509. [28] LATASH ML. The Hand: Shall We Ever Understand How It Works? Motor Control. 2015;19(2):108-126. [29] 林辉杰.掷铁饼动作中人体运动协调特征研究[D].上海:上海体育学院,2013. [30] 辜禹,陈楠,刘倩,等.肌肉协同理论在小儿脑性瘫痪康复评定中的应用进展[J].中国康复理论与实践,2020,26(6):673-677. [31] PEREZ-NOMBELA S, BARROSO F, TORRICELLI D, et al. Modular control of gait after incomplete spinal cord injury: differences between sides. Spinal Cord. 2017; 55(1):79-86. [32] MILETI I, ZAMPOGNA A, SANTUZ A, et al. Muscle Synergies in Parkinson’s Disease. Sensors (Basel). 2020;20(11):3209. [33] NAZIFI MM, YOON HU, BESCHORNER K, et al. Shared and Task-Specific Muscle Synergies during Normal Walking and Slipping. Front Hum Neurosci. 2017;11:40. [34] SANTUZ A, AKAY T, MAYER W P, et al. Modular organization of murine locomotor pattern in the presence and absence of sensory feedback from muscle spindles. J Physiol. 2019;597(12):3147-3165. [35] FELDMAN AG. On the functional tuning of the nervous system in movement control or preservation of stationary pose. II. Adjustable parameters in muscles. Biofizika. 1966;11(3):498-508. [36] FELDMAN AG. Once more on the equilibrium-point hypothesis (lambda model) for motor control. J Mot Behav. 1986;18(1):17-54. [37] FELDMAN AG. Space and time in the context of equilibrium-point theory. Wiley Interdiscip Rev Cogn Sci. 2011;2(3):287-304. [38] FLASH T. The control of hand equilibrium trajectories in multi-joint arm movements. Biol Cybern. 1987;57(4-5):257-274. [39] FELDMAN A G, KRASOVSKY T, BANINA M C, et al. Changes in the referent body location and configuration may underlie human gait, as confirmed by findings of multi-muscle activity minimizations and phase resetting. Exp Brain Res. 2011; 210(1):91-115. [40] ASATRIAN D G, FEL’DMAN A G. On the functional structure of the nervous system during movement control or preservation of a stationary posture. I. Mechanographic analysis of the action of a joint during the performance of a postural task. Biofizika. 1965;10(5):837-846. [41] FELDMAN AG, LEVIN MF. The Equilibrium-Point Hypothesis—past, present and future. Adv Exp Med Biol. 2009;629:699-726. [42] LATASH ML. Motor synergies and the Equilibrium-Point Hypothesis. Motor Control. 2010;14(3):294-322. [43] POPESCU FC, RYMERI WZ. Implications of low mechanical impedance in upper limb reaching motion. Motor Control. 2003;7(4):323-327. [44] SAINBURG R L. Should the Equilibrium Point Hypothesis (EPH) be Considered a Scientific Theory? Motor Control. 2015;19(2):142-148. [45] LATASH M L. Fifty Years of Physics of Living Systems. Adv Exp Med Biol. 2016; 957:81-103. [46] DE SA FARDILHA F. Motor Control and Learning: A Behavioral Emphasis. Br J Sports Med. 2020;64:12. [47] FELDMAN A G, GOUSSEV V, SANGOLE A, et al. Threshold position control and the principle of minimal interaction in motor actions. Prog Brain Res. 2007;165:267-281. [48] PILON J F, FELDMAN AG. Threshold control of motor actions prevents destabilizing effects of proprioceptive delays. Exp Brain Res. 2006;174(2):229-239. [49] OSTRY DJ, FELDMAN AG. A critical evaluation of the force control hypothesis in motor control. Exp Brain Res. 2003;153(3):275-288. [50] 王爱文,罗冬梅.人体运动控制理论及计算模型的研究进展[J].体育科学, 2017,37(8):58-68. [51] MORASSO P, CASADIO M, MOHAN V, et al. Revisiting the body-schema concept in the context of whole-body postural-focal dynamics. Front Hum Neurosci. 2015;9:83. [52] SCHMIDT RA. A Schema Theory of Discrete Motor Skill Learning. Psychol Rev. 1975;82(4):225-260. [53] SHEA CH, WULF G. Schema theory: a critical appraisal and reevaluation. J Mot Behav. 2005;37(2):85-101. [54] NEWELL KM. Schema theory (1975): retrospectives and prospectives. Res Q Exerc Sport. 2003;74(4):383-388. [55] SHERWOOD DE, LEE TD. Schema theory: critical review and implications for the role of cognition in a new theory of motor learning. Res Q Exerc Sport. 2003;74(4):376-382. [56] MEIGH KM. A Novel Investigation of Generalized Motor Program Theory: Syllable Stress as a Motor-Class Variable. J Speech Lang Hear Res. 2017;60(6S):1685-1694. [57] PLANT KL, STANTON NA. The explanatory power of Schema Theory: theoretical foundations and future applications in Ergonomics. Ergonomics. 2013;56(1):1-15. [58] VAN OPSTAL AJ. Dynamic patterns: the self-organization of brain and behavior. J Cogn Neurosci. 1996;8(4):385-386. [59] KUGLER PN, TURVEY MT. Information, natural law, and the self-assembly of rhythmic movement. Hillsdale, NJ: Lawrence Erlbaum Associates, Inc, 1987. [60] 林辉杰,严波涛,刘占锋,等.运动协调的定量方法以及在专项技术分析领域的研究进展[J].体育科学,2012,32(3):81-91. [61] 李立,文椈,傅维杰.运动中动态系统视角下的变异性及稳定性[J].天津体育学院学报,2014,29(2):105-107+112. [62] KING AC, HANNAN KB. Segment Coordination Variability During Double Leg Bodyweight Squats at Different Tempos. Int J Sports Med. 2019;40(11):725-731. [63] HAMILL J, PALMER C, VAN EMMERIK RE. Coordinative variability and overuse injury. Sports Med Arthrosc Rehabil Ther Technol. 2012;4(1):45. [64] LATASH ML, SCHOLZ JP, SCHONER G. Toward a new theory of motor synergies. Motor Control. 2007;11(3):276-308. [65] SCHOLZ JP, SCHONER G. The uncontrolled manifold concept: identifying control variables for a functional task. Exp Brain Res. 1999;126(3):289-306. [66] LATASH M. There is no motor redundancy in human movements. There is motor abundance. Motor Control. 2000;4(3):259-260. [67] LATASH ML. Synergy. United Kingdom: Oxford University Press, 2008. [68] MARTIN V, SCHOLZ JP, SCHONER G. Redundancy, self-motion, and motor control. Neural Comput. 2009;21(5):1371-1414. [69] ALEXANDER RM. A minimum energy cost hypothesis for human arm trajectories. Biol Cybern. 1997;76(2):97-105. [70] CLARK DJ, TING LH, ZAJAC FE, et al. Merging of healthy motor modules predicts reduced locomotor performance and muscle coordination complexity post-stroke. J Neurophysiol. 2010;103(2):844-857. [71] CHEUNG VC, TUROLLA A, AGOSTINI M, et al. Muscle synergy patterns as physiological markers of motor cortical damage. Proc Natl Acad Sci U S A. 2012; 109(36):14652-14656. [72] 桂奇政,孟明,马玉良,等.基于肌肉协同激活模型的上肢关节运动连续估计[J].仪器仪表学报,2016,37(6): 1405-1412. [73] 杨毅,彭玉鑫,郝增明,等.复杂人体运动冗余控制的肌肉协同理论研究进展与展望[J].体育科学,2020,40(12):63-72. [74] 黄威,高云园,张迎春,等.基于非负矩阵分解和复杂网络的肌间耦合分析[J].航天医学与医学工程,2019,32(2):159-66. [75] STEELE KM, ROZUMALSKI A, SCHWARTZ MH. Muscle synergies and complexity of neuromuscular control during gait in cerebral palsy. Dev Med Child Neurol. 2015;57(12):1176-1182. [76] ROZUMALSKI A, STEELE KM, SCHWARTZ MH. Muscle synergies are similar when typically developing children walk on a treadmill at different speeds and slopes. J Biomech. 2017;64:112-119. [77] SAITO A, TOMITA A, ANDO R, et al. Similarity of muscle synergies extracted from the lower limb including the deep muscles between level and uphill treadmill walking. Gait Posture. 2018;59:134-139. [78] HUG F, TURPIN NA, GUEVEL A, et al. Is interindividual variability of EMG patterns in trained cyclists related to different muscle synergies? J Appl Physiol (1985). 2010;108(6):1727-1736. [79] TURPIN NA, GUEVEL A, DURAND S, et al. Effect of power output on muscle coordination during rowing. Eur J Appl Physiol. 2011;111(12):3017-3029. [80] KRISTIANSEN M, SAMANI A, MADELEINE P, et al. Effects of 5 Weeks of Bench Press Training on Muscle Synergies: A Randomized Controlled Study. J Strength Cond Res. 2016;30(7):1948-1959. [81] 林辉杰,严波涛,许崇高.基于Bernstein运动协调观的优秀女子铁饼运动员“神经-肌肉”协调能力特征研究[J].天津体育学院学报,2014,29(6):489-495. [82] RABBI MF, PIZZOLATO C, LLOYD DG, et al. Non-negative matrix factorisation is the most appropriate method for extraction of muscle synergies in walking and running. Sci Rep. 2020;10(1):8266. [83] ELMEUA GONZALEZ M, SARABON N. Muscle modes of the equestrian rider at walk, rising trot and canter. PLoS One. 2020;15(8):e0237727. [84] DICESARE CA, MINAI AA, RILEY MA, et al. Distinct Coordination Strategies Associated with the Drop Vertical Jump Task. Med Sci Sports Exerc. 2020;52(5):1088-1098. [85] NORDIN AD, DUFEK JS. Neuromechanical synergies in single-leg landing reveal changes in movement control. Hum Mov Sci. 2016;49:66-78. [86] LAMBERT-SHIRZAD N, VAN DER LOOS HF. On identifying kinematic and muscle synergies: a comparison of matrix factorization methods using experimental data from the healthy population. J Neurophysiol. 2017;117(1):290-302. [87] 于海阔,董立,杨昆,等.基于功能MRI扩散张量成像的联合独立成分分析对阿尔茨海默病的多模态评估[J].中华放射学杂志,2019,53(8):642-647. [88] 刘越,王梦星,杜小霞,等.基于独立成分分析的遗尿症儿童脑功能网络研究[J].中国医学物理学杂志,2021,38(3):382-386. [89] THONGPANJA S, PHINYOMARK A, QUAINE F, et al. Probability Density Functions of Stationary Surface EMG Signals in Noisy Environments. IEEE Trans Instrum Meas. 2016;65(7):1547-1557. [90] SAITO A, WATANABE K, AKIMA H. Coordination among thigh muscles including the vastus intermedius and adductor magnus at different cycling intensities. Hum Mov Sci. 2015;40:14-23. [91] DAVIS BL, VAUGHAN CL. Phasic behavior of EMG signals during gait: use of multivariate statistics. J Electromyogr Kinesiol. 1993;3(1):51-60. [92] TURPIN NA, URIAC S, DALLEAU G. How to improve the muscle synergy analysis methodology? Eur J Appl Physiol. 2021;121(4):1009-1025. [93] ANTUVAN CW, BISIO F, MARINI F, et al. Role of Muscle Synergies in Real-Time Classification of Upper Limb Motions using Extreme Learning Machines. J Neuroeng Rehabil. 2016;3(1):76. [94] 徐睿,梁循,齐金山,等.极限学习机前沿进展与趋势[J].计算机学报,2019, 42(7):1640-1670. [95] BELOUCHRANI A, ABED-MERAIM K, CARDOSO JF. A blind source separation technique using second-order statistics. IEEE Trans Signal Process. 1997;45(2):434-444. [96] STERGIOU N, HARBOURNE R, CAVANAUGH J. Optimal movement variability: a new theoretical perspective for neurologic physical therapy. J Neurol Phys Ther. 2006;30:120-129. [97] HAMILL J, HADDAD JM, MCDERMOTT WJ. Issues in quantifying Variability From a Dynamical Systems Perspective. J Appl Biomech. 2000;16(4):407-418. [98] KELSO JA, JEKA JJ. Symmetry breaking dynamics of human multilimb coordination. J Exp Psychol Hum Percept Perform. 1992;18(3):645-668. [99] GRIEVE DW, GEAR RJ. The relationships between length of stride, step frequency, time of swing and speed of walking for children and adults. Ergonomics. 1966; 9(5):379-399. [100] TEPAVAC D, FIELD-FOTE EC. Vector Coding: A Technique for Quantification of Intersegmental Coupling in Multicyclic Behaviors. J Appl Biomech. 2001;17(3): 259-370. [101] MAGILL RA, ANDERSON D. Motor Learning and Control Concepts and Applications. 11 ed. New York: McGraw-Hill Education, 2016. [102] SPARROW WA, DONOVAN E, VAN EMMERIK R, et al. Using relative motion plots to measure changes in intra-limb and inter-limb coordination. J Mot Behav. 1987; 19(1):115-129. [103] CHANG R, VAN EMMERIK R, HAMILL J. Quantifying rearfoot-forefoot coordination in human walking. J Biomech. 2008;41(14):3101-3105. [104] BUTTON C, WHEAT J, LAMB P. Why coordination dynamics is relevant for studying sport performance. Complex systems in sport. 2014:44-61. [105] HARRISON AJ, RYAN W, HAYES K. Functional data analysis of joint coordination in the development of vertical jump performance. Sports Biomech. 2007;6(2):199-214. [106] MULLINEAUX D R, BARTLETT RM, BENNETT S. Research design and statistics in biomechanics and motor control. J Sports Sci. 2001;19(10):739-760. [107] 张百发,周兴龙,席健夫,等.幼儿前滑步动作发展特征的函数型数据分析[J].体育科学,2019,39(11):48-56. [108] HUGHES G, WATKINS J. Lower limb coordination and stiffness during landing from volleyball block jumps. Res Sports Med. 2008;16(2):138-154. [109] WANG Y, WATANABE K, ASAKA T. Effect of dance on multi-muscle synergies in older adults: a cross-sectional study. BMC Geriatr. 2019;19(1):340. [110] BLACK DP, SMITH BA, WU J, et al. Uncontrolled manifold analysis of segmental angle variability during walking: preadolescents with and without Down syndrome. Exp Brain Res. 2007;183(4):511-521. [111] ZHOU T, ZHANG L, LATASH ML. Intentional and unintentional multi-joint movements: their nature and structure of variance. Neuroscience. 2015;289:181-193. |
| No related articles found! |
| Viewed | ||||||
|
Full text |
|
|||||
|
Abstract |
|
|||||